
【题目】 问题与探索
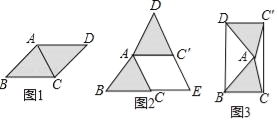
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
【答案】(1)菱形;(2)证明过程见解析
【解析】
试题分析:(1)、结论:菱形.首先证明四边形ACEC′是平行四边形,再由AC=AC′即可证明结论.
(2)、如图3中,过点A作AE⊥C′C于点E,首先证明DC′∥CB,DC′=BC,推出四边形BCC′D是平行四边形,再证明∠BCC′=900即可.
试题解析:(1)、结论:菱形.理由:如图2中,
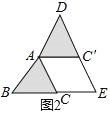
由题意∵AB=BC, ∴∠BAC=∠BCA=∠CAC′=∠AC′D ∴AC′∥EC, ∵∠CAC′=∠AC′D,
∴AC∥EC′, ∴四边形ACEC′是平行四边形, ∵AC=AC′, ∴四边形ACEC′是菱形.
(2)、如图3中,过点A作AE⊥C′C于点E,

由旋转的性质,得AC′=AC, ∴∠CAE=∠C′AE=![]() α=∠ABC,∠AEC=90°, ∵BA=BC,
α=∠ABC,∠AEC=90°, ∵BA=BC,
∴∠BCA=∠BAC ∴∠CAE=∠BCA, ∴AE∥BC. 同理,AE∥DC′, ∴BC∥DC′,
又∵BC=DC′, ∴四边形BCC′D是平行四边形, 又∵AE∥BC,∠AEC=90°,
∴∠BCC′=1800﹣900=900 ∴四边形BCC′D是矩形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a是一个两位数,b是一个三位数,把a放在b的右边组成一个五位数,用a,b的代数式表示所得的五位数是( )
A. ba B. 10b+a C. 10000b+a D. 100b+a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(3)(x+y)2(x﹣y)2
(4)(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)


图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com