
【题目】计算:
(1)|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(3)(x+y)2(x﹣y)2
(4)(x﹣2y+3z)(x+2y﹣3z)
【答案】解:(1))|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
=2﹣1+3﹣8
=﹣4;
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
=﹣4x8÷x6
=﹣4x2;
(3)原式=[(x+y)(x﹣y)]2
=(x2﹣y2)2
=x4﹣2x2y2+y4;
(4)(x﹣2y+3z)(x+2y﹣3z)
=x2﹣(2y﹣3z)2
=﹣x2﹣4y2+12yz﹣9z2 .
【解析】(1)直接利用绝对值以及零指数幂的性质和负整数指数幂分别化简求出答案;
(2)直接利用积的乘方运算法则以及结合同底数幂的乘除法运算法则求出答案;
(3)直接利用积的乘方运算法则求出答案;
(4)直接利用多项式乘法运算法则求出答案.
【考点精析】本题主要考查了零指数幂法则的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】有一道题目是一个多项式加上多项式xy﹣3yz﹣2xz,某同学以为是减去这个多项式,因此计算得到的结果为2xy﹣3yz+4xz.请你改正他的错误,求出正确的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(提示:正方形的四条边都相等,四个角都是直角)
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为______,线段CF、BD的数量关系为______;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足 条件时,CF⊥BC(点C、F不重合),并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 问题与探索
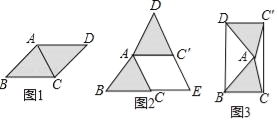
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
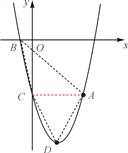
【题目】如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)连接AB、BC、CD、DA,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com