
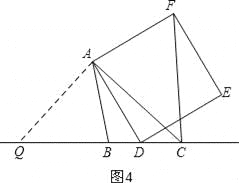
【题目】(10分)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(提示:正方形的四条边都相等,四个角都是直角)
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为______,线段CF、BD的数量关系为______;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足 条件时,CF⊥BC(点C、F不重合),并说明理由.

【答案】(1)垂直,相等;(2)45°
【解析】试题分析:(1)①证明△BAD≌△CAF,可得:BD=CF,∠B=∠ACF=45°,则∠BCF=∠ACB+∠ACF=90°,所以BD与CF相等且垂直;②①的结论仍成立,同理证明△DAB≌△FAC,可得结论:垂直且相等;
(2)、当∠ACB满足45°时,CF⊥BC;如图4,作辅助线,证明△QAD≌△CAF,即可得出结论.
试题解析:(1)、①CF与BD位置关系是垂直,数量关系是相等,
理由是: 如图2,∵四边形ADEF是正方形, ∴AD=AF,∠DAF=90°, ∴∠DAC+∠CAF=90°, ∵AB=AC,∠BAC=90°,∴∠BAD+∠DAC=90°,且∠B=∠ACB=45°,∴∠CAF=∠BAD, ∴△BAD≌△CAF,
∴BD=CF,∠B=∠ACF=45°, ∴∠ACB+∠ACF=45°+45°=90°,即∠BCF=90°,∴BC⊥CF,即BD⊥CF;
②当点D在BC的延长线上时,①的结论仍成立,理由是:
如图3,由正方形ADEF得AD=AF,∠DAF=90°, ∵∠BAC=90°, ∴∠DAF=∠BAC,
∴∠DAB=∠FAC, 又∵AB=AC, ∴△DAB≌△FAC, ∴CF=BD, ∠ACF=∠ABD,
∵∠BAC=90°,AB=AC, ∴∠ABC=45°, ∴∠ACF=∠ABC=45° ∴∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD;
(2)、当∠BCA=45°时,CF⊥BD,理由是: 如图4,过点A作AQ⊥AC,交BC于点Q, ∵∠BCA=45°, ∴∠AQC=45°, ∴∠AQC=∠BCA, ∴AC=AQ,
∵AD=AF,∠QAC=∠DAF=90°, ∴∠QAC﹣∠DAC=∠DAF﹣∠DAC, ∴∠QAD=∠CAF,
∴△QAD≌△CAF, ∴∠ACF=∠AQD=45°, ∠BCF=∠ACB+∠ACF=90°, 即CF⊥BD.


科目:初中数学 来源: 题型:
【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1 , 黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完). 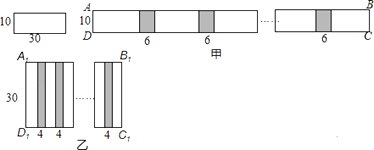
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步: ![]() =m;第二步:
=m;第二步: ![]() =k;第三步:分别用3、4、5乘以k,得三边长”.
=k;第三步:分别用3、4、5乘以k,得三边长”.
(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图8,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积.
(2)现有一张长为6.5cm,宽为2cm的纸片,如图9,请你将它分割成6块,再拼合成一个正方形.(要求:先在图9中画出分割线,再画出拼成的正方形并标明相应数据)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a是一个两位数,b是一个三位数,把a放在b的右边组成一个五位数,用a,b的代数式表示所得的五位数是( )
A. ba B. 10b+a C. 10000b+a D. 100b+a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(3)(x+y)2(x﹣y)2
(4)(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点B(﹣2,2),过反比例函数y=![]() (x<0,常数k<0)图象上一点A(﹣
(x<0,常数k<0)图象上一点A(﹣![]() ,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
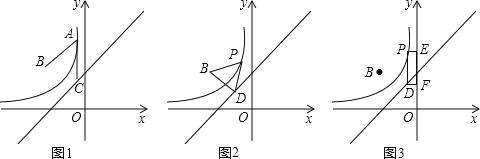
(1)分别求出m、k的值,并写出这个反比例函数解析式;
(2)发现:过函数y=![]() (x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系 ;
(x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系 ;
应用:①如图2,连接BD,当△PBD是等边三角形时,求此时点P的坐标;
②如图3,分别过点P、D作y的垂线交y轴于点E、F,问是否存在点P,使得矩形PEFD的周长取得最小值?若存在,请求出此时点P的坐标及矩形PEFD的周长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com