
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У���B����2��2����������������y=![]() ��x��0������k��0��ͼ����һ��A����
��x��0������k��0��ͼ����һ��A����![]() ��m����y���ƽ���߽�ֱ��l��y=x+2�ڵ�C����AC=AB��
��m����y���ƽ���߽�ֱ��l��y=x+2�ڵ�C����AC=AB��
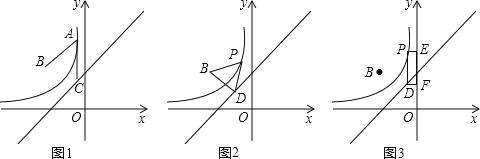
��1���ֱ����m��k��ֵ����д�������������������ʽ��
��2�����֣�������y=![]() ��x��0��ͼ��������һ��P����y���ƽ���߽�ֱ��l�ڵ�D����ֱ��д���㷢�ֵ�PB��PD��������ϵ ��
��x��0��ͼ��������һ��P����y���ƽ���߽�ֱ��l�ڵ�D����ֱ��д���㷢�ֵ�PB��PD��������ϵ ��
Ӧ�ã�����ͼ2������BD������PBD�ǵȱ�������ʱ�����ʱ��P�����ꣻ
����ͼ3���ֱ����P��D��y�Ĵ��߽�y���ڵ�E��F�����Ƿ���ڵ�P��ʹ�þ���PEFD���ܳ�ȡ����Сֵ�������ڣ��������ʱ��P�����꼰����PEFD���ܳ����������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() ��x��0����2��PB=PD����1��
��x��0����2��PB=PD����1��![]() ��
��![]() +1���������ڣ�����1��2����4
+1���������ڣ�����1��2����4
��������
�����������1�����AC��AB�ı���ʽ������AC=AB���m��ֵ��Ȼ�����ô���ϵ�������k��ֵ���ɣ�
��2����P����m��![]() ����m��0������D����m����m+2�������ݹ��ɶ������PB�ij����ɣ�������PBD�ǵȱ������Σ����ǵõ�PB=BD=PD�����ݵȱ������ε����ʵõ���2��m��=
����m��0������D����m����m+2�������ݹ��ɶ������PB�ij����ɣ�������PBD�ǵȱ������Σ����ǵõ�PB=BD=PD�����ݵȱ������ε����ʵõ���2��m��=![]() ��
��![]() +m��2����ã�m=3��
+m��2����ã�m=3��![]() ����m=
����m=![]() ��1�����ǵõ�P��
��1�����ǵõ�P��![]() ��3��
��3��![]() ����P��1��
����P��1��![]() ��
��![]() +1�����ڸ��ݾ��ε��ܳ��ļ��㹫ʽ�õ�����PEFD���ܳ�=��
+1�����ڸ��ݾ��ε��ܳ��ļ��㹫ʽ�õ�����PEFD���ܳ�=��![]() ��
��![]() ��2+4�����ݶ��κ��������ʼ��ɵõ����ۣ�
��2+4�����ݶ��κ��������ʼ��ɵõ����ۣ�
�����������1��AC=m��![]() ��AB=
��AB=![]() ��
��
��AC=AF��
��m=4��
����A����![]() ��4����
��4����
��k=��2��
��y=��![]() ��x��0����
��x��0����
��2����P����m��![]() ����m��0������D��m��m+2����
����m��0������D��m��m+2����
��PD=![]() ������m+2��=
������m+2��=![]() +m��2��
+m��2��
BP=![]() =
=![]() +m��2��
+m��2��
��PD=PB��
�ʴ�Ϊ��PB=PD��
���ߡ�PBD�ǵȱ������Σ�
��PB=BD=PD��
��PD��y�ᣬ
����2��m��=![]() ��
��![]() +m��2��
+m��2��
��![]() +m��2=
+m��2=![]() ��
��
��m=3��![]() ����m=
����m=![]() ��1��
��1��
��P��1��![]() ��
��![]() +1����
+1����
�ڴ𣺴����������������ĵ�P��
��P����m��![]() ����m��0������D����m����m+2����
����m��0������D����m����m+2����
������PEFD���ܳ�=2��PD+PE��=2��![]() +m��2+m��=
+m��2+m��=![]() +4m��4=��
+4m��4=��![]() ��
��![]() ��2+4��
��2+4��
����![]() ��
��![]() =0����m=2ʱ��P����1��2��ʱ������PEFD���ܳ�ȡ����СֵΪ4��
=0����m=2ʱ��P����1��2��ʱ������PEFD���ܳ�ȡ����СֵΪ4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(10��)��ͼ1���ڡ�ABC�У���ACBΪ��ǣ���DΪ����BC��һ�㣬����AD����ADΪһ������AD���Ҳ���������ADEF������ʾ�������ε������߶���ȣ��ĸ��Ƕ���ֱ�ǣ�
��1�����AB=AC����BAC=90�㣬
�ٵ���D���߶�BC��ʱ�����B���غϣ�����ͼ2���߶�CF��BD����ֱ�ߵ�λ�ù�ϵΪ______���߶�CF��BD��������ϵΪ______��
�ڵ���D���߶�BC���ӳ�����ʱ����ͼ3�����еĽ����Ƿ���Ȼ��������˵�����ɣ�
��2�����AB��AC����BAC����ǣ���D���߶�BC�ϣ�����ACB���� ����ʱ��CF��BC����C��F���غϣ�����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�ijƷ�Ƶ�ϴ��Һ���ս������50%���ۣ��ٴ�������ۣ��Կɻ���30Ԫ����������Ʒ�Ľ�����_____Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
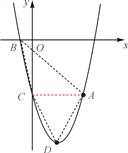
����Ŀ����ͼ��������y��ax2��bx��5(a��0)������A(4����5)����x��ĸ����ύ�ڵ�B����y�ύ�ڵ�C����OC��5OB�������ߵĶ���Ϊ��D.
(1)�����������ߵı���ʽ��
(2)����AB��BC��CD��DA�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�е���2�����ѿ�����ȫ��Լ332000m����332000��ѧ��������ʾӦΪ��������
A. 0.332��106 B. 3.32��105 C. 33.2��104 D. 332��103
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
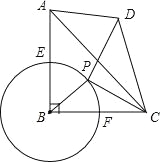
����Ŀ����ͼ���ڵ���ֱ��������ABC�У���ABC=90�㣬AB=BC=4����B��AB��BC����E��F����P�ǻ�EF�ϵ�һ�����㣬����PC���߶�PC��P����ʱ����ת90�㵽PD������CD��AD��
��1����֤����BPC�ס�ADC��
��2�����ı���ABCD����AD��CB�������Ϊ12ʱ������B�İ뾶��
��3������B�İ뾶��Ϊ2������P�ػ�EF�ӵ�E�˶�����PC����B����ʱ�����D���˶�·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������е�________������_________���ݵIJ�����������ݵļ�������ܹ���ӳ���ݵı仯_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����ͯ��ǰϦ��ij���������ֽ��ƴͼ������ߣ���֪����1�в�ֽ��2��ƴͼ����50Ԫ������2�в�ֽ��3��ƴͼ����80Ԫ��
��1��һ�в�ֽ��һ��ƴͼ�ļ۸���Ƕ���Ԫ��
��2��������������������߹�50�У�Ҫ���ֲ�Ʒ��Ҫ�����ҹ����ܽ��ܳ���850Ԫ�����ٹ����ֽ���ٺУ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com