
分析 根据x:y=5:2,设x=5k,则y=2k,然后代入M和N即可求值,然后求得M-N的值.
解答 解:∵x:y=5:2,
∴设x=5k,则y=2k.
则M=$\frac{20{k}^{2}}{25{k}^{2}-4{k}^{2}}$=$\frac{20{k}^{2}}{21{k}^{2}}$=$\frac{20}{21}$,N=$\frac{25{k}^{2}+4{k}^{2}}{25{k}^{2}-4{k}^{2}}$=$\frac{29{k}^{2}}{21{k}^{2}}$=$\frac{29}{21}$,
则M-N=$\frac{20}{21}$-$\frac{29}{21}$=-$\frac{9}{21}$=-$\frac{3}{7}$.
点评 本题考查了分式的化简求值,正确根据x:y=5:2,把x和y用k表示是本题的关键.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$cos45°=2sin30° | B. | tan30°•sin60°=sin245° | ||
| C. | cos45°-sin45°=0 | D. | sin(30°+45°)=sin30°+sin45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
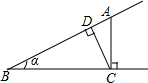 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )| A. | $\frac{CD}{BC}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{AD}{AC}$ | D. | $\frac{CD}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com