
| A. | $\sqrt{2}$cos45°=2sin30° | B. | tan30°•sin60°=sin245° | ||
| C. | cos45°-sin45°=0 | D. | sin(30°+45°)=sin30°+sin45° |
分析 根据特殊角三角函数值,可得答案.
解答 解:A、$\sqrt{2}$×cos45°=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,2sin30°=2×$\frac{1}{2}$=1,故A正确;
B、tan30°•sin60°=$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$,sin245°=($\frac{\sqrt{2}}{2}$)2=1,故B正确;
C、cos45°-sin45°=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=0,故C正确;
D、sin(30°+45°)<sin90°=1,sin30°+sin45°=$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$=$\frac{1+\sqrt{2}}{2}$>1,故D错误;
故选:D.
点评 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键,注意sin(α+β)<sinα+sinβ.


科目:初中数学 来源: 题型:解答题
 如图,A、B两地都是海上观测站,从A地观测,发现它的北偏东60°方向有一艘船,同时,在B地发现这艘船在它北偏东45°,试在图中确定这艘船的位置.
如图,A、B两地都是海上观测站,从A地观测,发现它的北偏东60°方向有一艘船,同时,在B地发现这艘船在它北偏东45°,试在图中确定这艘船的位置.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,AB=12,AD=5,以点A为圆心,r为半径作圆.
在矩形ABCD中,AB=12,AD=5,以点A为圆心,r为半径作圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
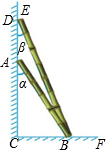 如图,有两根竹竿AB、DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.
如图,有两根竹竿AB、DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com