
 在矩形ABCD中,AB=12,AD=5,以点A为圆心,r为半径作圆.
在矩形ABCD中,AB=12,AD=5,以点A为圆心,r为半径作圆. 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$cos45°=2sin30° | B. | tan30°•sin60°=sin245° | ||
| C. | cos45°-sin45°=0 | D. | sin(30°+45°)=sin30°+sin45° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在梯形ABCD中,AD∥BC,EF∥BC,EF分别交AB,CD,AC于点E、F、G.若$\frac{CF}{FD}$=$\frac{2}{3}$,则$\frac{BE}{EA}$=$\frac{2}{3}$,$\frac{CG}{CA}$=$\frac{2}{5}$,$\frac{AG}{AC}$=$\frac{3}{5}$,$\frac{AB}{EB}$=$\frac{5}{2}$.
如图,在梯形ABCD中,AD∥BC,EF∥BC,EF分别交AB,CD,AC于点E、F、G.若$\frac{CF}{FD}$=$\frac{2}{3}$,则$\frac{BE}{EA}$=$\frac{2}{3}$,$\frac{CG}{CA}$=$\frac{2}{5}$,$\frac{AG}{AC}$=$\frac{3}{5}$,$\frac{AB}{EB}$=$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
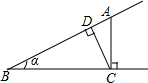 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )| A. | $\frac{CD}{BC}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{AD}{AC}$ | D. | $\frac{CD}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,坐标系中正方形网格的单位长度为1,抛物线y1=-$\frac{1}{2}{x^2}$+3向下平移2个单位后得抛物线y2,则阴影部分的面积S=4.
如图,坐标系中正方形网格的单位长度为1,抛物线y1=-$\frac{1}{2}{x^2}$+3向下平移2个单位后得抛物线y2,则阴影部分的面积S=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com