
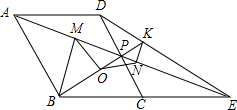
 ��ͼ������ABCD�У���P��CD���е㣬��BCD=60�㣬����AP��BC���ӳ����ڵ�E������BP��DE�ڵ�K����O���߶�BK���е㣬��BM��AE�ڵ�M����KN��AE�ڵ�N������MO��NO�������ĸ����ۣ��١�OMN�ǵ��������Σ���tan��OMN=$\frac{\sqrt{3}}{3}$����BP=4PK����PM•PA=3PD2��������ȷ���ǣ�������
��ͼ������ABCD�У���P��CD���е㣬��BCD=60�㣬����AP��BC���ӳ����ڵ�E������BP��DE�ڵ�K����O���߶�BK���е㣬��BM��AE�ڵ�M����KN��AE�ڵ�N������MO��NO�������ĸ����ۣ��١�OMN�ǵ��������Σ���tan��OMN=$\frac{\sqrt{3}}{3}$����BP=4PK����PM•PA=3PD2��������ȷ���ǣ�������| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �٢ۢ� | D�� | �ڢۢ� |
���� �������ε����ʵõ�AD��BC������ƽ���ߵ����ʵõ���Ӧ����ȣ�����ȫ�������ε��ж�������ADP�ա�ECP�������������ε����ʵõ�AD=CE����PI��CE��DE��I�����ݵ�P��CD���е�֤��CE=2PI��BE=4PI���������������ε����ʵõ�$\frac{KP}{KB}=\frac{PI}{BE}$=$\frac{1}{4}$���õ�BP=3PK���ʢ۴�����OG��AE��G������ƽ���ߵȷ��߶ζ����õ�MG=NG����OG��MN��֤����MON�ǵ��������Σ��ʢ���ȷ������ֱ�������ε����ʺ�������Ǻ��������OMN=$\frac{\sqrt{3}}{3}$���ʢ���ȷ��Ȼ�������Ӱ���������Ǻ������ɵõ�PM•PA=3PD2���ʢ���ȷ��
��� �⣺��PI��CE��DE��I��
���ı���ABCDΪ���Σ�
��AD��BC��
���DAP=��CEP����ADP=��ECP��
�ڡ�ADP�͡�ECP�У�
$\left\{\begin{array}{l}{��DAP=��CEP}\\{��ADP=��ECP}\\{DP=CP}\end{array}\right.$��
���ADP�ա�ECP��
��AD=CE��
��$\frac{PI}{CE}=\frac{PD}{DC}$���ֵ�P��CD���е㣬
��$\frac{PI}{CE}$=$\frac{1}{2}$��
��AD=CE��
��$\frac{KP}{KB}=\frac{PI}{BE}$=$\frac{1}{4}$��
��BP=3PK��
�ʢ۴���
��OG��AE��G��
��BM�AAE��M��KN�AAE��N��
��BM��OG��KN��
�ߵ�O���߶�BK���е㣬
��MG=NG����OG��MN��
��OM=ON��
����MON�ǵ��������Σ��ʢ���ȷ��
������ã���BPC����AMB����ABPΪֱ�������Σ�
��BC=2����CP=1���ɹ��ɶ����ã�BP=$\sqrt{3}$��
��AP=$\sqrt{7}$��
���������������ʽ��BM=$\frac{2\sqrt{21}}{7}$��
�ߵ�O���߶�BK���е㣬
��PB=3PO��
��OG=$\frac{1}{3}$BM=$\frac{2\sqrt{21}}{21}$��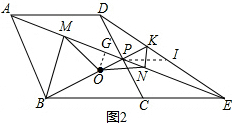
MG=$\frac{2}{3}$MP=$\frac{2}{7}$��
tan��OMN=$\frac{OG}{MG}$=$\frac{\sqrt{3}}{3}$���ʢ���ȷ��
�ߡ�ABP=90�㣬BM��AP��
��PB2=PM•PA��
�ߡ�BCD=60�㣬
���ABC=120�㣬
���PBC=30�㣬
���BPC=90�㣬
��PB=$\sqrt{3}$PC��
��PD=PC��
��PB2=3PD��
��PM•PA=3PD2���ʢ���ȷ��
��ѡB��
���� ���⿼��������ε����ʺ����������ε��ж������ʡ�ȫ�������ε��ж������ʣ���������ж����������ʶ����ǽ���Ĺؼ���ע��������Ǻ����ڽ����е����ã�


 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
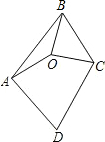 ��ͼ����֪O���ı���ABCD��һ�㣬OA=OB=OC����ABC=��ADC=70�㣬���DAO+��DCO�Ĵ�С�ǣ�������
��ͼ����֪O���ı���ABCD��һ�㣬OA=OB=OC����ABC=��ADC=70�㣬���DAO+��DCO�Ĵ�С�ǣ�������| A�� | 70�� | B�� | 110�� | C�� | 140�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
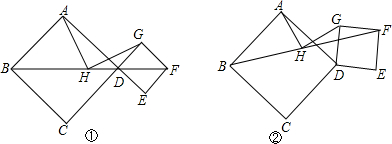
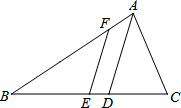 ��ͼ���ڡ�ABC�У���C=2��B��ADƽ�֡�BAC��BC�ڵ�D����EΪBC�е㣬EF��AD��AB�ڵ�F����BF=4AF��CD=$\frac{12}{5}$����AC=$\frac{18}{5}$��
��ͼ���ڡ�ABC�У���C=2��B��ADƽ�֡�BAC��BC�ڵ�D����EΪBC�е㣬EF��AD��AB�ڵ�F����BF=4AF��CD=$\frac{12}{5}$����AC=$\frac{18}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
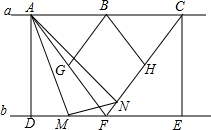 ��ͼ��ֱ��a��b����A��B��C��ֱ��a�ϣ�B�ǵ�AC�е㣬AC=4���ֱ����A��C��ֱ��b�Ĵ��ߣ�����ΪD��E��F��ֱ��b�ϵ�һ�����㣬����AF��CF����AF=CF��
��ͼ��ֱ��a��b����A��B��C��ֱ��a�ϣ�B�ǵ�AC�е㣬AC=4���ֱ����A��C��ֱ��b�Ĵ��ߣ�����ΪD��E��F��ֱ��b�ϵ�һ�����㣬����AF��CF����AF=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{-19}$ | B�� | $\sqrt{5a}$ | C�� | $\sqrt{{a}^{2}+1}$ | D�� | $\root{3}{9}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com