
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多 往返一趟.已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货车出发所用时间x(h)之间的函数关系图象.
往返一趟.已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货车出发所用时间x(h)之间的函数关系图象.
(1)①请在下图中画出货车距离甲地的路程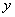 (km)与所用时间
(km)与所用时间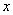 ( h)的函数关系图象;②两车在中途相遇次.
( h)的函数关系图象;②两车在中途相遇次.
(2)试求货车从乙地返回甲地时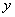 (km)与所用时间
(km)与所用时间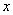 ( h)的函数关系式.
( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离乙地多少km?
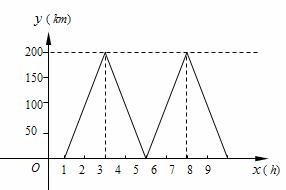
解:(1)①图象如图所示;…………1分
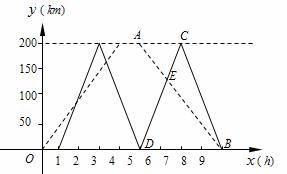
②3次;……………2分
(2)法一:如图,设直线AB表示的函数关系式为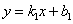 ,
,
∵图象过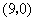 ,
,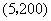 ,
,
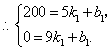
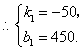
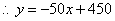 .①
.①
∴货车从乙地返回甲地时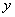 (km)与所用时间
(km)与所用时间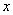 ( h)的函数关系式为y=-50x+450.
( h)的函数关系式为y=-50x+450.
……………5分
法二:∵货车的速度为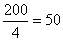 km/h ……………3分
km/h ……………3分
∴货车从乙地返回甲地时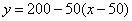
即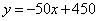 ……………5分
……………5分
(3)法一:设直线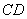 表示的函数关系式为
表示的函数关系式为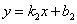 ,
,
∵图象过(5,0),(7,200),
∴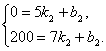
∴
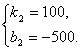 ∴y=100x-500.②……………6分
∴y=100x-500.②……………6分
由①,②组成方程组,解得: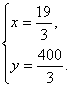 ……………7分
……………7分
∴所用时间为:t=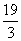 -5=
-5=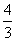 ,货车离乙地的距离为:S=200-
,货车离乙地的距离为:S=200-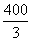 =
=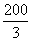 .……9分
.……9分
法二:设快递车第2次从甲出发到与返程的货车相遇所用时间为t小时,
则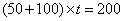 ,解得
,解得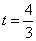 ……………7分
……………7分
∴货车离乙地 的距离为:
的距离为: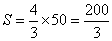 km.………………9分
km.………………9分


科目:初中数学 来源: 题型:
根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | 0.01 | 0.02 | 0.04 |
A.0 B.1 C.2 D.1或2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平行四边形ABCD中,M,N分别是AB,CD的中点,将四边形MBCN沿直线MN折叠后得到四边形MB′C′N,MB′与DN交于点P.若∠A=64°,则∠MPN=__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
根据下列已知条件,能画出惟一△ABC的是( )
A.AB=4,BC=5,CA=10 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45 °,AB=4 D.∠C=90°,AB=6
°,AB=4 D.∠C=90°,AB=6
查看答案和解析>>
科目:初中数学 来源: 题型:
如图8,在△ABC中,AA′,BB′分别是△ABC的外角∠EAB,∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为( )
A. 25° B. 30° C. 12° D. 18°

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,已知在平面直角坐标系中,正△OBC的边长和等腰直角△DEF的底边都为6,点E与坐标原点O重合,点D、B在x轴上,连结FC,△DEF沿x轴的正方向以每秒 个单位运动时,边EF所在直线和边OC所在直线相交于G,设运动时间为t.
个单位运动时,边EF所在直线和边OC所在直线相交于G,设运动时间为t.
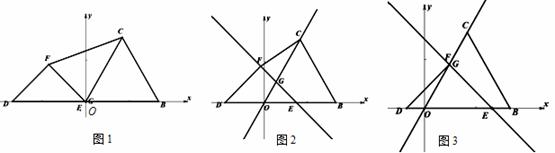
(1)如图2,当t=1时,①求OE的长;②求∠FGC的度数;③求G点坐标;
(2)如图3,当t为多少时,点F恰在△OBC的OC边上;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com