练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

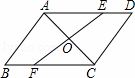
    如图，AC是▱ABCD的一条对角线，过AC中点O的直线分别交AD，BC于点E，F．

    （1）求证：△AOE≌△COF；

    （2）当EF与AC满足什么条件时，四边形AFCE是菱形？并说明理由．


    ∴四边形AFCE是菱形．

     （1）证明：∵四边形ABCD是平行四边形，

    ∴AD∥BC，

    ∴∠EAO=∠FCO，

    ∵O是OA的中点，

    ∴OA=OC，

    在△AOE和△COF中，，

    ∴△AOE≌△COF（ASA）；

    （2）解：EF⊥AC时，四边形AFCE是菱形；理由如下：

    ∵△AOE≌△COF，

    ∴AE=CF，

    ∵AE∥CF，

    ∴四边形AFCE是平行四边形，

    ∵EF⊥AC，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一个不等式组中的两个不等式的解集如图所示，则这个不等式组的解集为（　　）

    　  A．﹣1＜x≤2    B． ﹣1≤x＜2       C． ﹣1＜x＜2       D． 无解

    查看答案和解析>>

    科目：初中数学 来源： 题型：


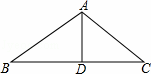
    如图，厂房屋顶人字架的跨度BC=10m．D为BC的中点，上弦AB=AC，∠B=36°，求中柱AD和上弦AB的长（结果保留小数点后一位）．

    参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式：2a2﹣2=　   　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式组，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，投掷这样的骰子一次，向上一面点数是偶数的结果有

       A.1种            B. 2种          C. 3种          D．6种

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3，某个函数的图象由线段AB和BC组成，其中点

       A（0，），B（1，），C（2，），则此函数的最小值是

    A．0       B．      C．1       D．                         图3

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点A（－2，n）在抛物线y＝x2＋bx＋c上．

       （1）若b＝1，c＝3，求n的值；

       （2）若此抛物线经过点B（4，n），且二次函数y＝x2＋bx＋c的最小值是－4，请画出点

    P（x－1，x2＋bx＋c）的纵坐标随横坐标变化的图象，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将正方形纸片以适当的方式折叠一次，沿折痕剪开后得到两块小纸片，用这两块小纸片拼接成一个新的多边形（不重叠、无缝隙），给出以下结论：

    ①可以拼成等腰直角三角形；

    ②可以拼成对角互补的四边形；

    ③可以拼成五边形；

    ④可以拼成六边形．

    其中所有正确结论的序号是　　．

    查看答案和解析>>

    同步练习册答案