
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
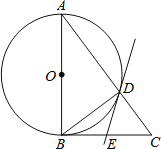
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,tanA=![]() ,求线段CD的长.
,求线段CD的长.
【答案】(1) DE与⊙O相切; 理由见解析;(2)![]() .
.
【解析】
(1)连接OD,利用圆周角定理以及等腰三角形的性质得出OD⊥DE,进而得出答案;
(2)得出△BCD∽△ACB,进而利用相似三角形的性质得出CD的长.
解:(1)直线DE与⊙O相切.
理由如下:连接OD.
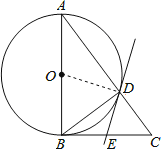
∵OA=OD
∴∠ODA=∠A
又∵∠BDE=∠A
∴∠ODA=∠BDE
∵AB是⊙O直径
∴∠ADB=90°
即∠ODA+∠ODB=90°
∴∠BDE+∠ODB=90°
∴∠ODE=90°
∴OD⊥DE
∴DE与⊙O相切;
(2)∵R=5,
∴AB=10,
在Rt△ABC中
∵tanA=![]()
∴BC=ABtanA=10×![]() ,
,
∴AC=![]() ,
,
∵∠BDC=∠ABC=90°,∠BCD=∠ACB
∴△BCD∽△ACB
∴![]()
∴CD=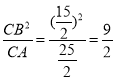 .
.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
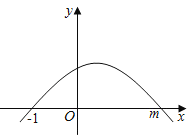
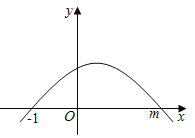
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
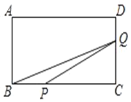
【题目】如图,已知矩形ABCD中,AB=4cm,BC=8cm.动点P在边BC上从点B向C运动,速度为1cm/s;同时动点Q从点C出发,沿折线C→D→A运动,速度为2cm/s.当一个点到达终点时,另一个点随之停止运动。设点P运动的时间为t(s),△BPQ的面积为S(cm2),则描述S(cm2)与时间t(s)的函数关系的图象大致是( )
A.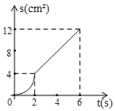 B.
B.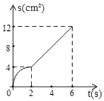
C.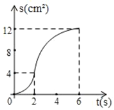 D.
D.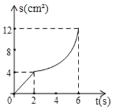
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
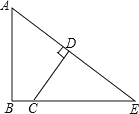
(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com