
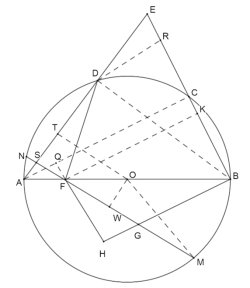
【题目】已知:等腰![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、点
、点![]() .
.
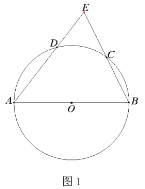
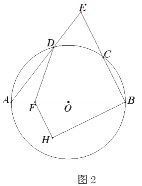
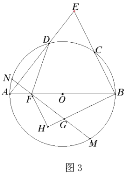
(1)如图1,求证:点![]() 为弧
为弧![]() 的中点;
的中点;
(2)如图2,点![]() 为直径
为直径![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交过点
,交过点![]() 且垂直于
且垂直于![]() 的直线于点
的直线于点![]() ,连接
,连接![]() ,
,![]() ,设
,设![]()
![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如图3,在(2)的条件下,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]()
![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)见详解;(2)m=n+45;(3)![]()
【解析】
(1)连接AC,根据题意知,∠ACB=90°,由AB=AE,等腰三角形三线合一可得AC平分∠BAE,相等的圆周角所对的弧相等即可证得;
(2)根据FH∥BC,推出∠ABE=∠BFH=∠CED=m°,由外角性质知DFB=∠A+∠ADF,利用三角形内角和180°以及∠DFH=135°,代换可得m与n的函数关系式;
(3)设∠DAC=∠BAC=![]() ,由(2)的结论可推出MN⊥AD,通过△BER≌△FGH,FG=DE,再利用勾股定理计算WM,可得出MN=2WM即可得结果.
,由(2)的结论可推出MN⊥AD,通过△BER≌△FGH,FG=DE,再利用勾股定理计算WM,可得出MN=2WM即可得结果.
(1)连接AC,
∵ AB是直径,
∴∠ACB=90°,
∵AB=AE,
∴AC平分∠BAE,
∴∠BAC=∠EAC,
∴点C是弧BD的中点;
(2)∵AB=AE,FH∥BC,
∴∠BFH=∠EBA=∠E=m°,∠A=180°-2m°,
∵∠ADF=n°,
∴∠BFD=∠A+∠ADF=180°-2m°+n°,
又∵∠DFH=135°,∠DFH=∠BFH+∠BFD,
∴135°=m°+180°-2m°+n°,
∴m=45+n,
∴m与n的函数关系式为:m=45+n,
故答案为:m=45+n;
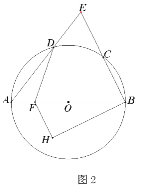
(3)设∠DAC=∠BAC=![]() ,
,
由(2)∠CED=∠ADF+45°,
∴∠ADF=90°-![]() -45°=45°-
-45°=45°-![]() ,
,
∴∠DFB=45°-![]() +2
+2![]() =45°+
=45°+![]() ,
,
∵∠BFM+2∠BFD=180°,
∴∠BFM=90°-2![]() ,
,
∵∠BFH=∠AFQ=90°-![]() ,
,
∴∠HFG=90°-![]() -(90°-2
-(90°-2![]() )=
)=![]() ,
,
∴∠BFG+∠E=180°,
∴∠ESM=90°,即MN⊥AD,
导角:∠FDB=∠DFB=45°+![]() ,
,
∴BF=BD,
又∵∠E=∠BFH=90°-![]() ,
,
∴∠DBR=∠FBH=![]() ,
,
∴△BDR≌△BHF,
∴FH=DR,
可推出△BER≌△FGH,
∴FG=DE,
∵FG:AB=2:5,
∴DE:AE=2:5,
设DE=2![]() ,AE=5
,AE=5![]() =AB,
=AB,
∴AD=3![]() ,BD=4
,BD=4![]() ,
,
∴tan2![]() =
=![]() ,tan
,tan![]() =
=![]() ,
,
∴tan∠ADF=tan(45°-![]() )=
)=![]() ,
,
∵CB-FH=CK=QF=4,
∴AF=4![]() ,
,
∴SF=![]() ×4=
×4=![]() ,
,
AS=![]() ×3=
×3=![]() ,
,
DS=![]() ×3=
×3=![]() ,
,
AD=AS+DS=12![]() ,
,
∴TD-![]() AD=6
AD=6![]() ,
,
∴ST=OW=DS-DT=![]() ,
,
∴AB=![]() ×5=20
×5=20![]() ,
,
∴r=10![]() ,
,
∴WM=![]() =
=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
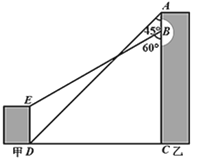
【题目】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:![]() ,
,![]() ,精确到0.1m.)
,精确到0.1m.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+2的图象与y轴交于A点,与x轴交于B点,⊙P的半径为
x+2的图象与y轴交于A点,与x轴交于B点,⊙P的半径为![]() ,其圆心P在x轴上运动.
,其圆心P在x轴上运动.
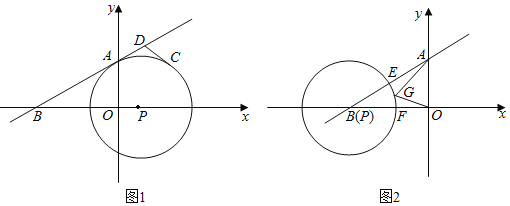
(1)如图1,当圆心P的坐标为(1,0)时,求证:⊙P与直线AB相切;
(2)在(1)的条件下,点C为⊙P上在第一象限内的一点,过点C作⊙P的切线交直线AB于点D,且∠ADC=120°,求D点的坐标;
(3)如图2,若⊙P向左运动,圆心P与点B重合,且⊙P与线段AB交于E点,与线段BO相交于F点,G点为弧EF上一点,直接写出![]() AG+OG的最小值 .
AG+OG的最小值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点F,BH⊥AB于点B,点M是BC的中点,连接FM并延长交BH于点H.

(1)如图①所示,若∠ABC=30°,求证:DF+BH=![]() BD;
BD;
(2)如图②所示,若∠ABC=45°,如图③所示,若∠ABC=60°(点M与点D重合),猜想线段DF、BH与BD之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 直径,
直径,![]() 点为半径
点为半径![]() 上异于
上异于![]() 点和
点和![]() 点的一个点,过
点的一个点,过![]() 点作与直径
点作与直径![]() 垂直的弦
垂直的弦![]() ,连接
,连接![]() ,作
,作![]() ,
,![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() 、
、![]() ,
,![]() 交
交![]() 于
于![]() 点.
点.
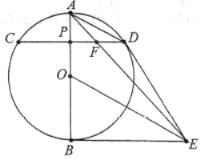
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() ;
;
(3)请猜想![]() 与
与![]() 的数量关系,并加以证明.
的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P,Q同时从点C出发,均以1cm/s的速度运动,其中点P沿CA向终点A运动;点Q沿CB向终点B运动.过点P作PE∥BC,分别交AD,AB于点E,F,设动点Q运动的时间为t秒.
(1)求DQ的长(用含t的代数式表示);
(2)以点Q,D,F,E为顶点围成的图形面积为S,求S与t之间的函数关系式;
(3)连接PQ,若点M为PQ中点,在整个运动过程中,直接写出点M运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,要在某东西走向的A、B两地之间修一条笔直的公路,在公路起点A处测得某农户C在A的北偏东68°方向上.在公路终点B处测得该农户c在点B的北偏西45°方向上.已知A、B两地相距2400米.
(1)求农户c到公路B的距离;(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
(2)现在由于任务紧急,要使该修路工程比原计划提前4天完成,需将该工程原定的工作效率提高20%,求原计划该工程队毎天修路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=![]() (x>0)的图象于点B1,B2,B3,…Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2……,记△B1P1B2的面积为S1,△B2P2B3的面积为S2……,△B6P6B7的面积为S6,则S1+S2+S3+…+S6=______________.
(x>0)的图象于点B1,B2,B3,…Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2……,记△B1P1B2的面积为S1,△B2P2B3的面积为S2……,△B6P6B7的面积为S6,则S1+S2+S3+…+S6=______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com