
分析 利用二次函数的性质以及抛物线与x轴的交点坐标逐一分析得出答案即可.
解答 解:①抛物线y=ax2+bx+c一定经过一个定点(-1,0),则0=a-b+c,即b=a+c,此选项成立成立;
②因为抛物线y=cx2+bx+a,c≠0,△>0,所以抛物线y=cx2+bx+a与x轴必有两个不同的交点,此选项成立成立;
③当b=2a+3c,则b2-4ac=(2a+3b)2-4ac=4a2+8ac+9b2=4(a+c)2+5c2,而a≠0,于是b2-4ac>0,则方程必有两个不相等的实数根;
④当a>0,b>a+c,
若c≥0,则b2-4ac>(a+c)2-4ac=(a-c)2≥0,此时抛物线y=ax2+bx+c与x轴两个不同的交点;
若c<0,则-2ac>0,b2-4ac>0,抛物线y=ax2+bx+c与x轴两个不同的交点
综上,抛物线y=ax2+bx+c与x轴必有两个不同的交点,结论成立.
正确的结论是①②③④.
故答案为:①②③④.
点评 此题考查抛物线与x轴的交点坐标,二次函数的性质,掌握二次函数与一元二次方程的关系,一元二次方程根与系数的关系及二次函数的性质是解决问题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
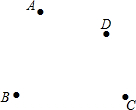 如图,平面上有A,B,C,D四个点,按照下列要求画图:
如图,平面上有A,B,C,D四个点,按照下列要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
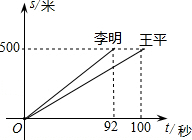 读图填空:如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,
读图填空:如图这是李明、王平两人在一次赛跑中,路程s与时间t的关系,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
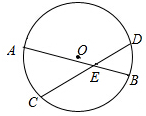 如图,AB,CD是⊙O的两条弦,交于点E,$\widehat{AC}$=80°,$\widehat{BD}$=60°,则∠BED=70°.
如图,AB,CD是⊙O的两条弦,交于点E,$\widehat{AC}$=80°,$\widehat{BD}$=60°,则∠BED=70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化(千人) | +0.6 | +0.8 | -0.4 | +0.6 | -0.8 | +0.2 | -1.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com