Question

2．某校学生会为了解该校学生擅长乐器的情况，随机抽取了n名学生进行问卷调查（要求每位学生只能填写一种自己最擅长的乐器），并将调查的结果绘制成如下的两幅不完整的统计图．
请根据图中提供的信息，解答下面的问题：
（1）这次参加调查的学生人数n为200；在扇形图中，表示“其他乐器”的扇形的圆心角为54度．
（2）将条形统计图补充完整．
（3）若该校共有1800名学生，请估计擅长“小提琴”乐器的学生人数．

Answer 1

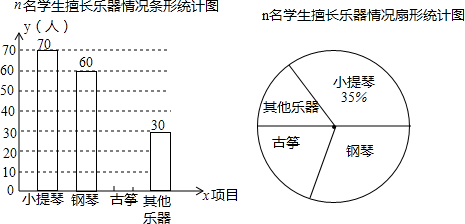
分析 （1）根据参加小提琴的人数除以参加小提琴所占的比重等于参加的总人数，可得答案；
根据圆周角乘以其他乐器所占的比重，可得答案；
（2）根据总人数减去小提琴的人数，钢琴的人数，其他乐器的人数，可得答案；
（3）根据总人数乘以小提琴人数所占的比重，可得答案．

解答 解：（1）这次参加调查的学生人数n为70÷35%=200人，
表示“其他乐器”的扇形的圆心角为360°×$\frac{30}{200}$=54°．
故答案为：200，54；

（2）参加古筝的人数为200-70-60-30=40．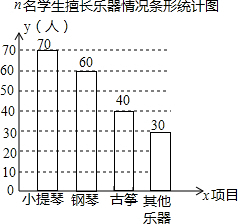
；

（3）擅长“小提琴”的学生1800×35%=630（人）．
答：若该校有1800名学生，则估计擅长“小提琴”的学生共有630人．

点评 本题考查了条形统计图，利用参加小提琴的人数除以参加小提琴所占的比重得出参加的总人数是解题关键．