
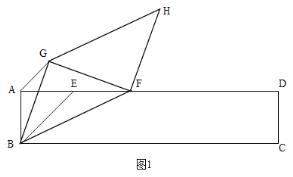
【题目】如图,矩形ABCD,AB=2,BC=10,点E为AD上一点,且AE=AB,点F从点E出发,向终点D运动,速度为1cm/s,以BF为斜边在BF上方作等腰直角△BFG,以BG,BF为邻边作BFHG,连接AG.设点F的运动时间为t秒.
(1)试说明:△ABG∽△EBF;
(2)当点H落在直线CD上时,求t 的值;
(3)点F从E运动到D的过程中,直接写出HC的最小值.

【答案】(1)证明见解析;(2)![]() ;(3)HC最小值是
;(3)HC最小值是![]()
【解析】
(1)根据两边成比例夹角相等即可证明两三角形相似;
(2)构建如图2平面直角坐标系,作HM⊥AD于M,GN⊥AD于N.设AM交BG于K.首先证明△GFN≌△FHM,想办法求出点H的坐标,构建方程即可解决问题;
(3)由(2)可知H(2![]() t,4
t,4![]() t),令x=2
t),令x=2![]() t,y=4
t,y=4![]() t,消去t得到y
t,消去t得到y![]() .推出点H在直线y
.推出点H在直线y![]() 上运动,根据垂线段最短即可解决问题.
上运动,根据垂线段最短即可解决问题.
(1)如图1.
∵△ABE,△BGF都是等腰直角三角形,∴![]() .
.
∵∠ABE=∠GBF=45°,∴∠ABG=∠EBF,∴△ABG∽△EBF.
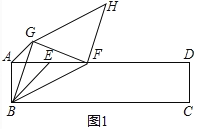
(2)如图2构建如图平面直角坐标系,作HM⊥AD于M,GN⊥AD于N.设AM交BG于K.
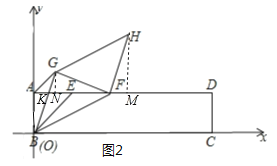
∵△GFH是等腰直角三角形,∴FG=FH,∠GNF=∠GFH=∠HMF=90°,∴∠GFN+∠HFM=90°,∠HFM+∠FHM=90°,∴∠GFN=∠FHM,∴△GFN≌△FHM,∴GN=FM,FN=HM.
∵△ABG∽△EBF,∴![]() ,∠AGB=∠EFB.
,∠AGB=∠EFB.
∵∠AKG=∠BKF,∴∠GAN=∠KBF=45°.
∵EF=t,∴AG![]() t,∴AN=GN=FM
t,∴AN=GN=FM![]() t,∴AM=2
t,∴AM=2![]() t,HM=FN=2
t,HM=FN=2![]() t,∴H(2
t,∴H(2![]() t,4
t,4![]() t),当点H在直线CD上时,2
t),当点H在直线CD上时,2![]() t=10,解得:t
t=10,解得:t![]() .
.
(3)由(2)可知H(2![]() t,4
t,4![]() t),令x=2
t),令x=2![]() t,y=4
t,y=4![]() t,消去t得到y
t,消去t得到y![]() ,∴点H在直线y
,∴点H在直线y![]() 上运动,如图3,作CH垂直直线y
上运动,如图3,作CH垂直直线y![]() 垂足为H.
垂足为H.
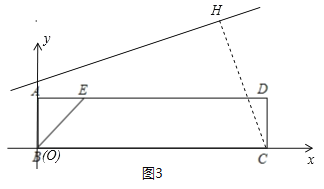
根据垂线段最短可知,此时CH的长最小,易知直线CH的解析式为y=﹣3x+30,由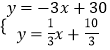 ,解得:
,解得:![]() ,∴H(8,6).
,∴H(8,6).
∵C(10,0),∴CH![]() ,∴HC最小值是2
,∴HC最小值是2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
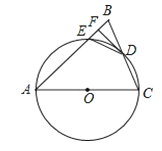
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
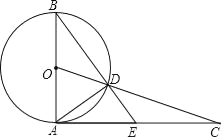
【题目】如图,AB是⊙O的直径,点C为⊙O外一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E,∠CDE=∠CAD.
(1)求证:CD2=ACEC;
(2)判断AC与⊙O的位置关系,并证明你的结论;
(3)若AE=EC,求tanB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进A、B两种型号的电动自行车共30辆,其中每辆B型电动自行车比每辆A型电动自行车多500元.用5万元购进的A型电动自行车与用6万元购进的B型电动自行车数量一样.
(1)求A、B两种型号电动自行车的进货单价;
(2)若A型电动自行车每辆售价为2800元,B型电动自行车每辆售价为3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.写出y与m之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学考试中,小明有一道选择题(只能在四个选项A、B、C、D中选一个)不会做,便随机选了一个答案;小亮有两道选择题都不会做,他也随机选了两个答案.
(1)小明随机选的这个答案,答对的概率是 ;
(2)通过画树状图或列表法求小亮两题都答对概率是多少?
(3)这个班数学老师参加集体阅卷,在阅卷的过程中,发现学生的错误率较高.他想:若这10道选择题都是靠随机选择答案,则这10道选择题全对的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是不等边三角形
分别是不等边三角形![]() (即
(即![]() )的边
)的边![]() 、
、![]() 的中点.
的中点.![]() 是
是![]() 平面上的一动点,连接
平面上的一动点,连接![]() 、
、![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,顺次连接点
的中点,顺次连接点![]() 、
、![]() 、
、![]() 、
、![]() .
.
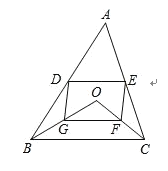
(1)如图,当点![]() 在
在![]() 内时,求证:四边形
内时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若连接![]() ,且满足
,且满足![]() ,
,![]() .问此时四边形
.问此时四边形![]() 又是什么形状?并请说明理由.
又是什么形状?并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲按顺时针方向环形,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第一次相遇在AD边上,请问它们第2015次相遇在( )边上.
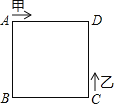
A. ADB. DCC. BCD. AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化商店计划同时购进A、B两种仪器,若购进A种仪器2台和B种仪器3台,共需要资金1700元;若购进A种仪器3台,B种仪器1台,共需要资金1500元.
(1)求A、B两种型号的仪器每台进价各是多少元?
(2)已知A种仪器的售价为760元/台,B种仪器的售价为540元/台.该经销商决定在成本不超过30000元的前提下购进A、B两种仪器,若B种仪器是A种仪器的3倍还多10台,那么要使总利润不少于21600元,该经销商有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
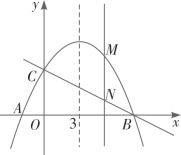
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧),与y轴交于C点.
x+4的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧),与y轴交于C点.
(1)求抛物线的解析式;
(2)求A,B两点的坐标;
(3)若M是抛物线上B,C两点之间的一个动点(不与B,C重合),过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com