

分析 (1)由翻折的性质可知BC′=BC=13,C′E=EC,在Rt△ABC′中由勾股定理可求得AC′的长,得到C′D=1,设DE=x,则C′E=5-x,最后在Rt△C′DE中由勾股定理列出关于x的方程求解即可;
(2)在△ABD中由勾股定理可求得BD=$\sqrt{194}$,由翻折的性质可知BC′=BC=13,C′E=EC,先求得C′D=$\sqrt{194}-13$,然后证明△C′DE∽△ABD,由相似三角形的性质可求得DE的长.
解答 解:(1)由翻折的性质可知:BC′=BC=13,C′E=EC.
∵在Rt△ABC′中由勾股定理得:AC′=$\sqrt{BC{′}^{2}-A{B}^{2}}$=12.
∴C′D=13-12=1.
设DE=x,则C′E=5-x.
在Rt△C′DE中由勾股定理可知:C′E2=DE2+C′D2.即(5-x)2=x2+12.
解得:x=$\frac{12}{5}$.
∴DE的长为$\frac{12}{5}$.
(2)在Rt△ABD中,由勾股定理得BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{194}$.
∵由翻折的性质可知BC′=BC=13,C′E=EC,
∴C′D=$\sqrt{194}-13$.
∵∠EDC′=∠ABD,∠EC′D=∠A=90°,
∴△C′DE∽△ABD.
∴$\frac{C′D}{AB}=\frac{DE}{BD}$,即$\frac{\sqrt{194}-13}{5}=\frac{DE}{\sqrt{194}}$.
解得:DE=$\frac{194-13\sqrt{194}}{5}$.
点评 本题主要考查的是翻折变换、勾股定理的应用、相似三角形的判定和性质,由勾股定理列出关于x的方程以及由相似三角形的性质得到$\frac{\sqrt{194}-13}{5}=\frac{DE}{\sqrt{194}}$是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{5}$ | D. | $\sqrt{5}$:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量m(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
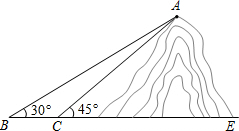 如图,小明想测山高和索道的长度,他在B处仰望山顶A,测得仰角∠B=30°.再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=45°.
如图,小明想测山高和索道的长度,他在B处仰望山顶A,测得仰角∠B=30°.再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com