
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,![]() 于D、E两点,在射线l上取点F,使FC=FD.
于D、E两点,在射线l上取点F,使FC=FD.
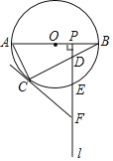
(1)求证:FC是⊙O的切线;
(2)当点E是![]() 的中点时,
的中点时,
① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若![]() ,且AB=20,求OP的长.
,且AB=20,求OP的长.
【答案】(1)见解析;(2)①以O,B,E,C为顶点的四边形是菱形.理由见解析,②6.
【解析】
(1)连接OC,根据等边对等角及∠OBC+∠BDP=90°,证明∠OCB+∠FCD=90°即可;
(2)①四边形BOCE是菱形,证明△BOE,△OCE均为等边三角形,得到四条边相等,进而证明四边形BOCE是菱形;
②由![]() ,可求得AC=12,BC=16,由垂径定理可求出BH;利用三角形面积的不同表示方法求得PE=8,再利用勾股定理可求出OP的长.
,可求得AC=12,BC=16,由垂径定理可求出BH;利用三角形面积的不同表示方法求得PE=8,再利用勾股定理可求出OP的长.
解:(1)证明:连接OC,
∵OB=OC,
∴∠OBC=∠OCB,
∵PF⊥AB,
∴∠BPD=90°,
∴∠OBC+∠BDP=90°,
∵FC=FD
∴∠FCD=∠FDC
∵∠FDC=∠BDP
∴∠OCB+∠FCD=90°
∴OC⊥FC
∴FC是⊙O的切线;
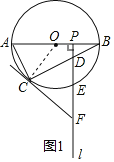
(2)如图2,连接OC,OE,BE,CE,
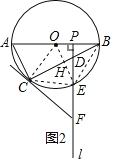
①以O,B,E,C为顶点的四边形是菱形.
理由如下:
∵AB是直径,∴∠ACB=90°,
∵∠BAC=60°,∴∠BOC=120°,
∵点E是![]() 的中点,
的中点,
∴∠BOE=∠COE=60°,
∵OB=OE=OC,
∴△BOE,△OCE均为等边三角形,
∴OB=BE=CE=OC,
∴四边形BOCE是菱形;
②∵![]() ,设AC=3k,BC=4k(k>0),
,设AC=3k,BC=4k(k>0),
由勾股定理得AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,
∴AC=12,BC=16,
∵点E是![]() 的中点,
的中点,
∴OE⊥BC,BH=CH=8,
∴![]() OE×BH=
OE×BH=![]() OB×PE,即10×8=10PE,解得:PE=8,
OB×PE,即10×8=10PE,解得:PE=8,
由勾股定理得OP=![]() =
=![]() =6.
=6.


科目:初中数学 来源: 题型:
【题目】已知:抛物线y=(m-1)x2+mx+m2-4的图象经过原点,且开口向上.
(1)确定![]() 的值;
的值;
(2)求此抛物线的顶点坐标;
(3)画出抛物线的图象,结合图象回答:当![]() 取什么值时,
取什么值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
(4)结合图象直接回答:当![]() 取什么值时,
取什么值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应学习任务
旋转对称
把正n边形绕着它的中心旋转![]() 的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有
的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有![]() 的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.
的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.

任务:
(1)如图2,正六边形关于其中心O有 的旋转对称,中心对称图形关于其对称中心有 的旋转对称;
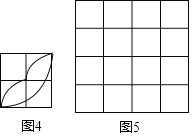
(2)图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转 与原图形重合;
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2与直线![]() 相交于A、B两点
相交于A、B两点
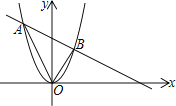
(1)求A、B两点的坐标
(2)点O为坐标原点,△AOB的面积等于___________
(3)当y1<y2时,x的取值范围是________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为16米,拱高(CD)为4米,求:
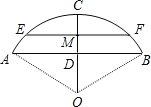
(1)桥拱半径.
(2)若大雨过后,桥下河面宽度(EF)为12米,求水面涨高了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 第一象限的图象上,连接
第一象限的图象上,连接![]() ,延长
,延长![]() 与双曲线的另一支交于点
与双曲线的另一支交于点![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
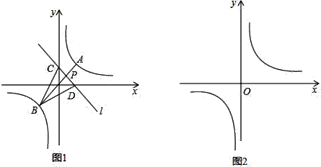
(1)在图![]() 中,当
中,当![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 三点的坐标,并求出直线
三点的坐标,并求出直线![]() 的解析式.
的解析式.
(2)当点![]() 的坐标为
的坐标为![]() 时,利用图
时,利用图![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,对称轴为直线
,对称轴为直线![]() .
.

![]() 求该二次函数的关系式和顶点坐标;
求该二次函数的关系式和顶点坐标;
![]() 结合图象,解答下列问题:
结合图象,解答下列问题:
①当![]() 时,求函数
时,求函数![]() 的取值范围.
的取值范围.
②当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
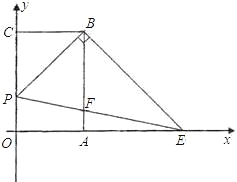
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=2时,求点E的坐标;
(2)若AB平分∠EBP时,求t的值.
(3)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com