
【题目】已知抛物线y1=x2与直线![]() 相交于A、B两点
相交于A、B两点
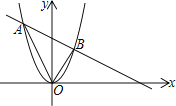
(1)求A、B两点的坐标
(2)点O为坐标原点,△AOB的面积等于___________
(3)当y1<y2时,x的取值范围是________________
科目:初中数学 来源: 题型:
【题目】爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题.
例如:![]()
![]() ;因此
;因此![]() 有最小值是1,只有当
有最小值是1,只有当![]() 时,才能得到这个式子的最小值1.
时,才能得到这个式子的最小值1.
同样![]() ,因此
,因此![]() 有最大值是8,只有当
有最大值是8,只有当![]() 时,才能得到这个式子的最大值8.
时,才能得到这个式子的最大值8.
(1)当x= 时,代数式﹣2(x﹣3)2+5有最大值为 .
(2)当x= 时,代数式2x2+4x+3有最小值为 .
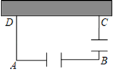
(3)矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的小门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB、OC、BD、CD.
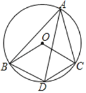
(1)求证:四边形OBDC是菱形;
(2)当∠BAC为多少度时,四边形OBDC是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
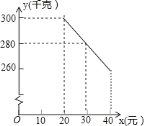
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,![]() 于D、E两点,在射线l上取点F,使FC=FD.
于D、E两点,在射线l上取点F,使FC=FD.
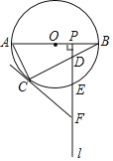
(1)求证:FC是⊙O的切线;
(2)当点E是![]() 的中点时,
的中点时,
① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若![]() ,且AB=20,求OP的长.
,且AB=20,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,且过点(1,0).顶点位于第二象限,其部分图像如图所示,给出以下判断:
,且过点(1,0).顶点位于第二象限,其部分图像如图所示,给出以下判断:
①![]() 且
且![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤直线![]() 与抛物线
与抛物线![]() 两个交点的横坐标分别为
两个交点的横坐标分别为![]() ,则
,则![]() .其中正确的个数有( )
.其中正确的个数有( )
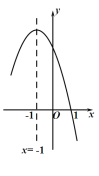
A. 5个B. 4个C. 3个D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
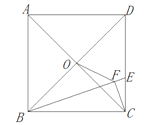
【题目】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点.点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com