
 ����ʦ������ʦ���˴�A�س����������г���ͬһ��·��ʻ��B�أ�����ʦ��Ϊ���£���A��ͣ��0.5Сʱ�������1Сʱ����������������Լ����˭�ȵ�B�ؾ���ԭ�صȴ�������������صľ���S����λ��km������ʻʱ��t����λ��h��֮��ĺ�����ϵ��ͼ����ͼ��ʾ��
����ʦ������ʦ���˴�A�س����������г���ͬһ��·��ʻ��B�أ�����ʦ��Ϊ���£���A��ͣ��0.5Сʱ�������1Сʱ����������������Լ����˭�ȵ�B�ؾ���ԭ�صȴ�������������صľ���S����λ��km������ʻʱ��t����λ��h��֮��ĺ�����ϵ��ͼ����ͼ��ʾ������ ��1��ͨ���۲�ͼ����Եó��߶�MN��ʾ��ʵ�����壻
��2��������������صľ����������ʦ��ʻ0.5h��·�̣�
��3������ʦ���غ���������е����������ɣ�
��4������ǰ���������1km�����������������ʦ����������ʦ��û�г�����������ʦͣ��ʱ����ʦ������
��� �⣺��1���߶�MN��ʾ����ʦ��ʻ;��ͣ����0.5h��
��2����ͼ��֪����ʦ��ʻ�ٶ�Ϊ��$\frac{30}{2-0.5}=20��km/h��$��
��������������صľ���Ϊ��20����1-0.5��=10��km����
��3������ʦ������ʦ������������صľ���S����ʻʱ��t֮��ĺ�����ϵʽΪ��S=kt+b��
����N��1��10������2.5��30������ã�
$\left\{\begin{array}{l}{k+b=10}\\{2.5k+b=30}\end{array}\right.�����\left\{\begin{array}{l}{k=\frac{40}{3}}\\{b=-\frac{10}{3}}\end{array}\right.$��
���ʱS��t�ĺ�����ϵʽΪ��$S=\frac{40}{3}t-\frac{10}{3}$��
������ʦ����B��ʱt=2��
�൱t=2ʱ��S=$\frac{40}{3}��2-\frac{10}{3}=\frac{70}{3}$��
��t=2ʱ������ʦ������ʦ��ľ���Ϊ��$30-\frac{70}{3}=\frac{20}{3}��km��$��
����ʦ��������ٶ�Ϊ��$\frac{30-10}{2.5-1}=\frac{40}{3}��km/h��$
������ʦ���غ���ҪxСʱ�����ٴ�������ʦ��������
$\frac{40}{3}x+20x=\frac{20}{3}�����x=\frac{1}{5}$��
��������ʦ����B�غ�������ԭ����ԭ·����A�أ�����Ҫ0.2h�����ٴ�������ʦ������
��4��������ǰ������ʦ���ٶ�Ϊ��10��0.5=20��km/h����
������ʦ����mСʱ���������1km�������������
��һ�֣�����ʦ����������ʦ��û�г�����$20m=1�����m=\frac{1}{20}$��
�ڶ��֣�����ʦͣ��ʱ����ʦ������$20m+1=10�����m=\frac{9}{20}$��
��������ǰ������ʦ����$\frac{1}{20}��\frac{9}{20}$Сʱ���������1km��
���� �����ص㿼����һ�κ���ͼ���ʵ��Ӧ�����ϵ����⣬������ʶ����ͼ������������˺����뷽�̵�˼�룮


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{10}$ | B�� | $\frac{1}{20}$ | C�� | $\frac{2}{25}$ | D�� | $\frac{1}{25}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
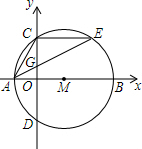 ��ͼ����ƽ��ֱ������ϵxOy�У���M��x���ϣ���M��x����A��B���㣬��y����C��
��ͼ����ƽ��ֱ������ϵxOy�У���M��x���ϣ���M��x����A��B���㣬��y����C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
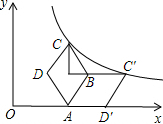 ��ͼ������ABCD�Ķ���A��x����������ϣ���DAB=60�㣬��������ABCD��AB���۵õ�����ABC��D�䣬D���ǡ������x���ϣ�˫����y=$\frac{k}{x}$��x��0��ǡ�þ�����C��C�䣬��C��CE��ֱC��B���ӳ�����E������CC�䣬��֪S��CEC��=$\frac{3\sqrt{3}}{2}$����k��ֵ�ǣ�������
��ͼ������ABCD�Ķ���A��x����������ϣ���DAB=60�㣬��������ABCD��AB���۵õ�����ABC��D�䣬D���ǡ������x���ϣ�˫����y=$\frac{k}{x}$��x��0��ǡ�þ�����C��C�䣬��C��CE��ֱC��B���ӳ�����E������CC�䣬��֪S��CEC��=$\frac{3\sqrt{3}}{2}$����k��ֵ�ǣ�������| A�� | 3 | B�� | 3$\sqrt{3}$ | C�� | 6$\sqrt{3}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com