
(12分)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是_________;(2分)
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是_________________.(2分)

(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.(5分)
(3)拓展探究
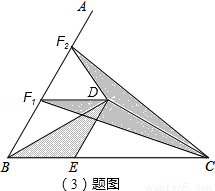
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).
若在射线BA上存在点F,使 ,请直接写出相应的BF的长:BF=_____.(3分)
,请直接写出相应的BF的长:BF=_____.(3分)

(1)①DE∥AC;②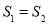 ;(2)成立,证明见试题解析;(3)
;(2)成立,证明见试题解析;(3)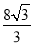 或
或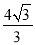 .
.
【解析】
试题分析:(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=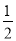 AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;
(3)过点D作DF1∥BE,求出四边形BEDF1是菱形,根据菱形的对边相等可得BE=DF1,然后根据等底等高的三角形的面积相等可知点F1为所求的点,过点D作DF2⊥BD,求出∠F1DF2=60°,从而得到△DF1F2是等边三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“边角边”证明△CDF1和△CDF2全等,根据全等三角形的面积相等可得点F2也是所求的点,然后在等腰△BDE中求出BE的长,即可得解.
试题解析:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,∴△ACD是等边三角形,∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;
②∵∠B=30°,∠C=90°,∴CD=AC=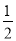 AB,∴BD=AD=AC,
AB,∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;
故答案为:DE∥AC;S1=S2;
(2)如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,
在△ACN和△DCM中,∵∠ACN=∠DCM,∠CMD=∠N=90°,AC=CD,∴△ACN≌△DCM(AAS),
∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;
(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,
此时S△DCF1=S△BDE;过点D作DF2⊥BD,∵∠ABC=60°,F1D∥BE,∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD=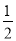 ∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,
∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等边三角形,∴DF1=DF2,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB=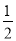 ×60°=30°,
×60°=30°,
∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,在△CDF1和△CDF2中,∵ DF1=DF2,∠CDF1=∠CDF2,CD=CD,
∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,
∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD=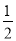 ×60°=30°,
×60°=30°,
又∵BD=4,∴BE=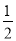 ×4÷cos30°=
×4÷cos30°=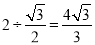 ,∴BF1=
,∴BF1=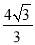 ,BF2=BF1+F1F2=
,BF2=BF1+F1F2=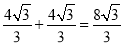 ,
,
故BF的长为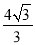 或
或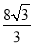 .
.
考点:全等三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年福建泉州惠安第三教区八年级上学期期中数学试卷(解析版) 题型:解答题
(9分)如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.

求证:(1)△AEF≌△BCD.
(2)∠C=∠E
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省南平市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是 _________ cm.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省、三中、城关小学九年级上学期期中联考数学试卷(解析版) 题型:选择题
若一元二次方程式 的两根为
的两根为 ,其中a、b为两数,则
,其中a、b为两数,则 之值为( )
之值为( )
A. B.
B. C.3 D.5
C.3 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省泉州市惠安第三教研片区九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列各组中的四条线段是成比例线段的是( )
A.a=6,b=4,c=10,d=5 B.a=3,b=7,c=2,d= 9
C.a=2,b=4,c=3,d=6 D.a=4,b=11,c=3,d=2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省、三中、城关小学九年级上学期期中联考数学试卷(解析版) 题型:解答题
(8分)如图,△AOB中,OA=OB,以O为圆心的圆经过AB上两点C、D,则AC与BD相等吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省泉州市惠安第三教研片区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(9分)如图,在梯形ABCD中,AD∥BC,∠B=∠ACD.

(1)证明:△ABC∽△DCA;
(2)若AC=6,BC=9,求AD长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中质量监测数学试卷(解析版) 题型:解答题
(7分)已知:关于x的方程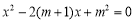
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个你喜欢的非零整数,使原方程有两个实数根,并求这两个实数根的平方和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com