
【题目】(问题背景)
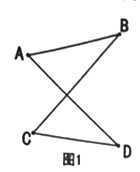
(1)如图1的图形我们把它称为“8字形”,请说理证明![]() .
.
(简单应用)
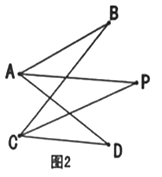
(2)如图2,![]() 分别平分
分别平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数(可直接使用问题(1)中的结论).
的度数(可直接使用问题(1)中的结论).
(问题探究)
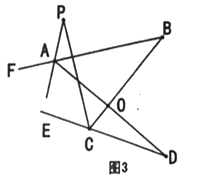
(3)如图3,直线![]() 平分
平分![]() 的外角
的外角![]() ,
,![]() 平分
平分![]() 的外角
的外角![]() ,若
,若![]() ,
,![]() ,猜想
,猜想![]() 的度数为 .
的度数为 .
(拓展延伸)
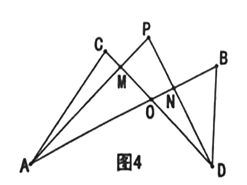
(4)在图4中,若设![]() ,
,![]() ,
,![]() ,试问
,试问![]() 与
与![]() 、
、![]() 之间的数量关系为: (用
之间的数量关系为: (用![]() 表示
表示![]() )
)
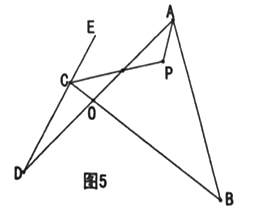
(5)在图5中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的关系,直接写出结论 .
的关系,直接写出结论 .
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() (4)
(4)![]() ;(5)
;(5)![]()
【解析】
(1)根据三角形内角和定理即可证明;
(2)如图2,根据角平分线的性质得到∠1=∠2,∠3=∠4,列方程组即可得到结论;
(3)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°-∠2,∠PCD=180°-∠3,由∠P+(180°-∠1)=∠D+(180°-∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解决问题;
(4)(5)同法列出方程组即可解决问题.
(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)解:如图2,∵AP、CP分别平分∠BAD,∠BCD,
∴∠1=∠2,∠3=∠4,
由(1)的结论得: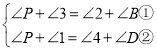 ,
,
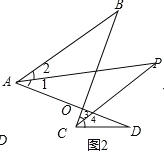
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D,
∴∠P=![]() (∠B+∠D)=23°;
(∠B+∠D)=23°;
(3)解:如图3,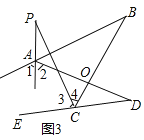
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°-∠2,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠D+(180°-∠3),
∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°;
×(36°+16°)=26°;
故答案为:26°;
【拓展延伸】
(4)同法可得:![]() ;
;
故答案为:![]() ,
,
(5)同法可得:![]() .
.
故答案为:![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】已知a、b、c在数轴上的位置如图所示,所对应的点分别为A、B、C,
![]()
(1)在数轴上表示2的点与表示5的点之间的距离为 ;
在数轴上表示﹣1的点与表示3的点之间的距离为 ;在数轴上表示﹣3的点与表示﹣5的点之间的距离为 ;由此可得点A、B之间的距离为 ,点B、C之间的距离为 ,点A、C之间的距离为 ;
(2)化简:﹣|a+b|+|c﹣b|﹣|b﹣a|;
(3)若c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣(a﹣4c﹣b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】
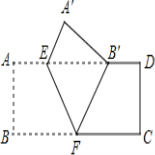
A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,BC=6,点E是AD边上一点,∠ABE=30°,BE=DE,连接BD.动点M从点E出发沿射线ED运动,过点M作MN∥BD交直线BE于点N.
(1)如图1,当点M在线段ED上时,求证:MN=![]() EM;
EM;
(2)设MN长为x,以M、N、D为顶点的三角形面积为y,求y关于x的函数关系式;
(3)当点M运动到线段ED的中点时,连接NC,过点M作MF⊥NC于F,MF交对角线BD于点G(如图2),求线段MG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
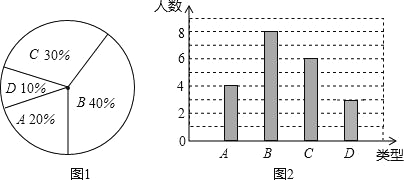
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2),请回答下列问题:
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点 E、F 分别在AB、CD上,EF∥BC,EF交BD于点G.若EG=5,DF=2,则图中两块阴影部分的面积之和为______.
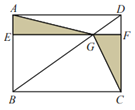
查看答案和解析>>
科目:初中数学 来源: 题型:
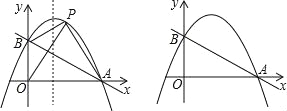
【题目】如图,直线y=﹣![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )

A. 10 B. 9 C. 8 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
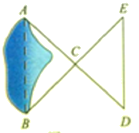
(1)DE=AB吗?请说明理由;
(2)如果DE的长度是8 m,则AB的长度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com