
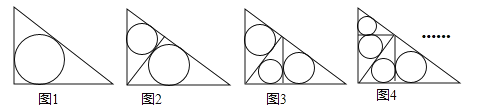
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .
【答案】π.
【解析】
试题分析:(1)图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F,则∠OEC=∠OFC=90°.
∵∠C=90°,∴四边形OECF为矩形.∵OE=OF,∴矩形OECF为正方形.
设圆O的半径为r,则OE=OF=r,AD=AE=3﹣r,BD=4﹣r,∴3﹣r+4﹣r=5,r=![]() =1,∴S1=
=1,∴S1=![]() =π;
=π;
(2)图2,由S△ABC=![]() ×3×4=
×3×4=![]() ×5×CD,∴CD=
×5×CD,∴CD=![]() .由勾股定理得:AD=
.由勾股定理得:AD=![]() =
=![]() ,BD=5﹣
,BD=5﹣![]() =
=![]() .
.
由(1)得:⊙O的半径=![]() =
=![]() ,⊙E的半径=
,⊙E的半径=![]() =
=![]() ,∴S1+S2=
,∴S1+S2=![]() =π;
=π;
(3)图3,由S△CDB=![]() =
=![]() ×4×MD,∴MD=
×4×MD,∴MD=![]() .由勾股定理得:CM=
.由勾股定理得:CM=![]() =
=![]() ,MB=
,MB=![]() =
=![]() .由(1)得:⊙O的半径=
.由(1)得:⊙O的半径=![]() ,:⊙E的半径=
,:⊙E的半径=![]() =
=![]() ,⊙F的半径=
,⊙F的半径=![]() =
=![]() ,∴S1+S2+S3=
,∴S1+S2+S3=![]() =π,∴图4中的S1+S2+S3+S4=π,则S1+S2+S3+…+S10=π.故答案为:π.
=π,∴图4中的S1+S2+S3+S4=π,则S1+S2+S3+…+S10=π.故答案为:π.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) 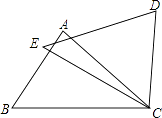
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=EC,∠A=∠D
D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
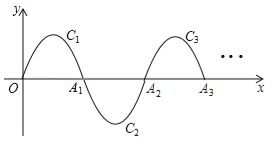
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
查看答案和解析>>
科目:初中数学 来源: 题型:
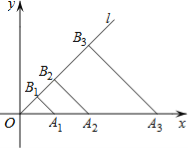
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn﹣1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是 ,B3的坐标是 ,Bn的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况,并将所得数据进行了统计,结果如图所示.
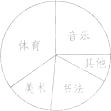
(1)在这次调查中,一共抽查了多少名学生?
(2)求出扇形统计图中参加“音乐”活动项目所对应的扇形的圆心角度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
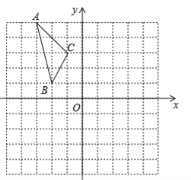
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A1B2C2关于原点O成中心对称图形,写出△A1B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A2B3C3,写出△A2B3C3的各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com