
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3
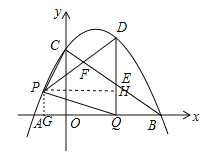
x+3![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x+3
x+3![]() ;(2)①P(
;(2)①P(![]() t﹣3,
t﹣3,![]() t),D(9﹣2t,﹣
t),D(9﹣2t,﹣![]() t2+
t2+![]() t),②
t),②![]() ;(3)t=3,F(
;(3)t=3,F(![]() ,
,![]() ).
).
【解析】试题分析:(1)先求出B、C两点的坐标,进而求出直线BC的函数表达式;
(2)①过点P作PG⊥x轴于点G ,由AO=3,BO=9,OC=![]() ,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=
,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=![]() ,PG=
,PG=![]() ,得到P的坐标.由OQ=
,得到P的坐标.由OQ=![]() ,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
②过点P作PG⊥x轴于点G,PH⊥QD于点H,得到四边形PGQH是矩形,从而有QD=2HQ=2PG,解关于t的方程即可;
(3)由中点坐标公式和F在直线BC上得到![]() ,解得t=3.把t=3代入得到F的坐标.
,解得t=3.把t=3代入得到F的坐标.
试题解析:(1)由y=0,得![]() ,解得:
,解得:![]() ,
,![]() ,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得
,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得![]() ,∴点C的坐标为(0,
,∴点C的坐标为(0,![]() ).
).
设直线BC的函数表达式为:![]() ,∴
,∴![]() ,解得:
,解得: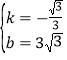 ,∴直线BC的函数表达式为:
,∴直线BC的函数表达式为:![]() ;
;
(2)①过点P作PG⊥x轴于点G .∵A(-3,0),B(9,0),C(0,![]() )∴AO=3,BO=9,OC=
)∴AO=3,BO=9,OC=![]() ,∴tan∠CAO=
,∴tan∠CAO=![]() ,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=
,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=![]() ,PG=
,PG=![]() ,∴OG=3-
,∴OG=3-![]() ,∴P(
,∴P(![]() ,
,![]() ).∵OQ=
).∵OQ=![]() ,∴D的横坐标为
,∴D的横坐标为![]() ,∵D在抛物线
,∵D在抛物线![]() 上,∴D的纵坐标为
上,∴D的纵坐标为![]() =
=![]() ,∴D D(
,∴D D(![]() ,
,![]() ).
).
综上所述:P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() );
);
②过点P作PG⊥x轴于点G,PH⊥QD于点H.∵QD⊥x轴,∴四边形PGQH是矩形,∴HQ=PG.∵PQ=PD,PH⊥QD,∴QD=2HQ=2PG.
∵P、D两点的坐标分别为P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∴
),∴![]() =
=![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ,∴当PQ=PD时,t的值为
,∴当PQ=PD时,t的值为![]() .
.
(3)∵F为PD的中点,且P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),由中点坐标公式得:F(
),由中点坐标公式得:F(![]() ,
,![]() ),∵F在直线BC上,∴
),∵F在直线BC上,∴![]() ,∴
,∴![]() ,解得:t=3.
,解得:t=3.
当t=3时,![]() =
=![]() ,
,![]() =
=![]() ,∴F(
,∴F(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】我们定义:在四边形中,一条边上的两个角称为邻角.如果一条边上的邻角相等,且这条边对边上的邻角也相等,则把这样的四边形叫做“完美四边形”.
初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是______;
问题探究:在完美四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求该完美四边形的周长与面积;
,求该完美四边形的周长与面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形BEFG都是正方形,设AB=a,DE=b(a>b).

(1)写出AG的长度(用含字母a、b的代数式表示);
(2)观察图形,试用不同的方法表示图形中阴影部分的面积,你能获得相应的一个因式分解公式吗?请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2.试利用⑵中的公式,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
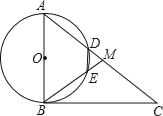
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.连结DE,使四边形DEBA为⊙O的内接四边形.
(1)求证:∠A=∠ABM=∠MDE;
(2)若AB=6,当AD=2DM时,求DE的长度;
(3)连接OD,OE,当∠A的度数为60°时,求证:四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来.
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”![]() 为了便于记忆,同学们可仿照图用双手表示“三线八角”
为了便于记忆,同学们可仿照图用双手表示“三线八角”![]() 两大拇指代表被截直线,食指代表截线
两大拇指代表被截直线,食指代表截线![]() 下列三幅图依次表示
下列三幅图依次表示![]()
![]()

A. 同位角、同旁内角、内错角B. 同位角、内错角、同旁内角
C. 同位角、对顶角、同旁内角D. 同位角、内错角、对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com