
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() 轴平分
轴平分![]() ,求
,求![]() _____.
_____.
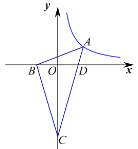
【答案】![]()
【解析】
要求k的值,通常可求A的坐标,可作x轴的垂线,构造相似三角形,利用CD=4AD和C(0,-4)可以求出A的纵坐标,再利用三角形相似,设未知数,由相似三角形对应边成比例,列出方程,求出待定未知数,从而确定点A的坐标,进而确定k的值.
解:过A作AE⊥x轴,垂足为E,
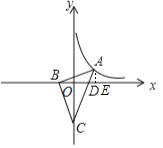
∵C(0,-4),
∴OC=4,
∵∠AED=∠COD=90°,∠ADE=∠CDO
∴△ADE∽△CDO,
![]() ,
,
∴AE=1;
又∵y轴平分∠ACB,CO⊥BD,
∴BO=OD,
∵∠ABC=90°,
∴∠OCD=∠DAE=∠ABE=∠BCE,
∵∠DOC=∠ADE=90°
∴△ABE~△COD,
∴![]()
设DE=n,则BO=OD=4n,BE=9n,
∴![]() ,
,
∴![]() ,
,
∴OE=5n=![]() ,
,
故点A(![]() ,1),
,1),
∴k=![]() ×1=
×1=![]()
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5![]() .请求出:
.请求出:

(1)∠AOC的度数;
(2)△OAC的面积;
(3)线段AD的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
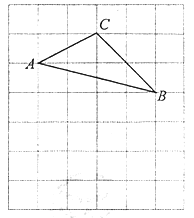
(I)计算![]() 的值等于____________;
的值等于____________;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边、面积等于![]() 的矩形,并简要说明画图方法(不要求证明)_____________.
的矩形,并简要说明画图方法(不要求证明)_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
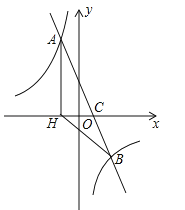
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n)
,点B的坐标为(4,n)
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市有![]() ,
,![]() 两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买
两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买![]() 型瓶3个或以上,一次性返还现金5元,设购买
型瓶3个或以上,一次性返还现金5元,设购买![]() 型瓶
型瓶![]() (个),所需总费用为
(个),所需总费用为![]() (元),则下列说法不一定成立的是( )
(元),则下列说法不一定成立的是( )
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
A.购买![]() 型瓶的个数是
型瓶的个数是![]() 为正整数时的值B.购买
为正整数时的值B.购买![]() 型瓶最多为6个
型瓶最多为6个
C.![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() D.小张买瓶子的最少费用是28元
D.小张买瓶子的最少费用是28元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 边以每秒1个单位长度的速度运动到点
边以每秒1个单位长度的速度运动到点![]() 时停止,连接
时停止,连接![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).

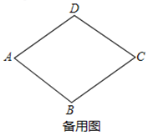
(1)菱形![]() 对角线
对角线![]() 的长为 ;
的长为 ;
(2)当点![]() 恰在
恰在![]() 上时,求t的值;
上时,求t的值;
(3)当![]() 时,求
时,求![]() 的周长;
的周长;
(4)直接写出在整个运动过程中,点![]() 运动的路径长.
运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
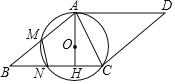
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com