
【题目】已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5![]() .请求出:
.请求出:

(1)∠AOC的度数;
(2)△OAC的面积;
(3)线段AD的长(结果保留根号).
【答案】(1)∠AOC=60°;(2)![]() ;(3)AD=
;(3)AD=![]() .
.
【解析】
(1)根据圆周角定理可得答案;
(2)证明△OAC是等边三角形,可知∠AOH=30°,解直角三角形求出AH即可解决问题;
(3)由切线的性质可得AD⊥OA,然后根据正切的概念求得AD的长.
解:(1)∵∠B=30°,
∴∠AOC=2∠B=60°;
(2)在△AOC中,∵OA=OC,∠AOC=60°,
∴△OAC是等边三角形,
∵OH⊥AC,
∴∠AOH=30°,
∵![]() ,
,
∴AH=OH·tan30°=![]() ,
,
∴AC=2AH=10,
∴![]() ;
;
(3)∵AD是切线,
∴AD⊥OA,
∵△OAC是等边三角形,∠AOC=60°,
∵tan60°=![]() ,OA=AC=10,
,OA=AC=10,
∴AD=OA·tan60°=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象分别位于第二、第四象限,
的图象分别位于第二、第四象限,![]() 、
、![]() 两点在该图象上,下列命题:①过点
两点在该图象上,下列命题:①过点![]() 作
作![]() 轴,
轴,![]() 为垂足,连接
为垂足,连接![]() .若
.若![]() 的面积为3,则
的面积为3,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() 其中真命题个数是( )
其中真命题个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“禹州钧瓷”名扬天下,某网店专门销售某种品牌的钧瓷花瓶,成本为40元/件,每天销量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
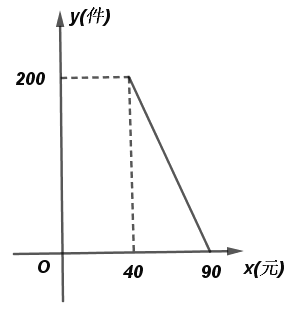
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)如果规定每天钧瓷花瓶的销售量不低于120件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少元?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为了保证捐款后每天剩余利润不低于2000元,试确定该钧瓷花瓶销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
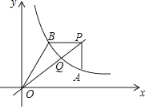
【题目】如图,直线y=mx与反比例函数![]() (x>0)的图象交于Q点,点B(3,4)在反比例函数
(x>0)的图象交于Q点,点B(3,4)在反比例函数![]() 的图象上,过点B作PB∥x轴交OQ于点P,过点P作PA∥y轴交反比例函数图象于点A.
的图象上,过点B作PB∥x轴交OQ于点P,过点P作PA∥y轴交反比例函数图象于点A.
(1)若点A的纵坐标为![]() ,求反比例函数及直线OP的解析式;
,求反比例函数及直线OP的解析式;
(2)连接OB,在(1)的条件下,求sin∠BOP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),则下列说法错误的是( )
A.a+c=0
B.无论a取何值,此二次函数图象与x轴必有两个交点,且函数图象截x轴所得的线段长度必大于2
C.当函数在x<![]() 时,y随x的增大而减小
时,y随x的增大而减小
D.当﹣1<m<n<0时,m+n<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作∠BCD=∠ACB交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:ED=EC;
(2)求证:AF是⊙O的切线;
(3)如图2,若点G是△ACD的内心,BCBE=25,求BG的长.
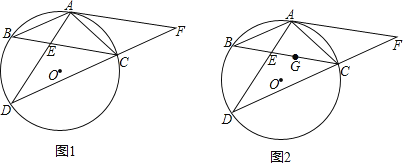
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购买50根跳绳,如果A型跳绳的数量不多于B型跳绳数量的3倍,那么A型跳绳最多能买多少条?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com