
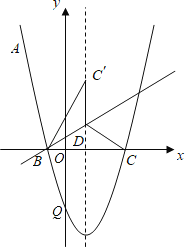
【题目】如图,抛物线y=ax2+bx﹣![]() 经过点A(﹣2,
经过点A(﹣2,![]() ),与x轴相交于B,C两点,且B点坐标为(﹣1,0).
),与x轴相交于B,C两点,且B点坐标为(﹣1,0).
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;
(3)抛物线与y轴交于点Q,连接BQ,DQ,在抛物线上有一个动点P,且S△PBD=S△BDQ,求满足条件的点P的横坐标.
【答案】(1)![]() ;(2)
;(2)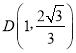 ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)利用待定系数法可求解析式;
(2)设对称轴于BC的交点为E,先求出点C,点E坐标,可求BC=4,BE=CE=2,由折叠的性质可得BC'的长,由勾股定理可求C'E,DE的长,即可求解;
(3)分两种情况讨论,利用等底等高的两个三角形的面积相等,可求解.
(1)将A(﹣2,![]() ),B(-1,0)代入y=ax2+bx﹣
),B(-1,0)代入y=ax2+bx﹣![]() 中,
中,
可得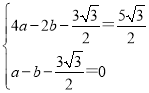 ,
,
∴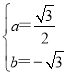 ,
,
∴![]() ;
;
(2)如图,设对称轴于BC的交点为E,
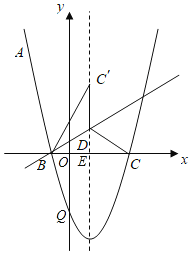
∵![]() 与x轴交于A,B两点,
与x轴交于A,B两点,
∴![]() ;
;
∴x1=-1,x2=3,
∴点C(3,0),
∴对称轴为直线x=1,
∴BE=CE=2,BC=4,
∵点D在抛物线的对称轴上,
∴BD=CD,
∵将△BCD沿直线BD翻折得到△BC′D,
∴BC=BC'=4,CD=C'D,
∴BD=C'D,
∴![]() ,
,
∴![]()
∵BD2=DE2+BE2,
∴![]() ,
,
∴![]() ,
,
∴点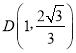 ;
;
(3)如图,设BD交y轴于点F,
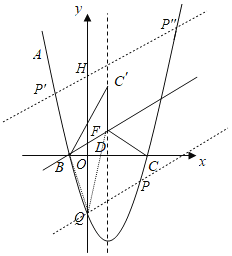
∵点B(-1,0),点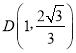 ,
,
∴直线BD解析式为:![]() ,
,
∴点 ,
,
∵抛物线的解析式为:![]() 与y轴交于点Q,
与y轴交于点Q,
∴点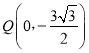 ,
,
∴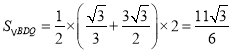 ,
,
若点Q,点P在BD的同侧时,
∵S△PBD=S△BDQ,
∴点P与点Q到直线BD的距离相等,即PQ∥BD,
∴直线PQ解析式为:![]() ,
,
∴![]() ,
,
∴x=0,![]() ,
,
∴点P的横坐标为![]() ;
;
若点P与点Q在BD的两侧时,
∵S△PBD=S△BDQ,
∴点P与点Q到直线BD的距离相等,
∵点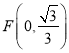 ,点
,点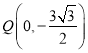 ,
,
∴![]() ,
,
在y轴上截取HF=FQ,过点H作BD的平行线交抛物线于点P'和P',
∴![]() ,
,
∴点H坐标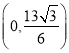 ,
,
∴直线HP'解析式为:![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述:当点P的横坐标为![]() 或
或![]() 或
或![]() 时,S△PBD=S△BDQ.
时,S△PBD=S△BDQ.


科目:初中数学 来源: 题型:
【题目】已知,如图AB是圆O的直径,射线AM⊥AB于点A.点D在AM上,连接OD交圆O于点E,过点D作DC=DA.交圆O于点C(A,C不重合),连接BC,CE.
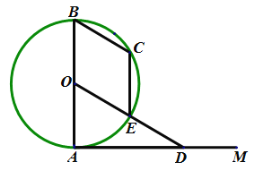
(1)求证:CD是圆O的切线;
(2)若四边形OECB是菱形,圆O的直径AB=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=1,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆交BC于D,过D作⊙O的切线EF交AC于E,交AB延长线于F.
(1)求证:DE⊥AC.
(2)若BD=2![]() ,tan∠CDE=
,tan∠CDE=![]() ,求BF的长.
,求BF的长.
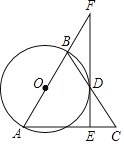
查看答案和解析>>
科目:初中数学 来源: 题型:
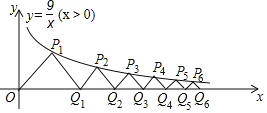
【题目】如图,在平面直角坐标系xOy中,点P1(x1,y1)、P2(x2,y2)、P3(x3,y3),……,Pn(xn,yn)均在反比例函数y=![]() (x>0)的图象上,点Q1、Q2、Q3、……、Qn均在x轴的正半轴上,且△OP1Q1、△Q1P2Q2、△Q2P3Q3、…、△Qn﹣1PnQn均为等腰直角三角形,OQ1、Q1Q2、Q2Q3、……、Qn﹣1Qn分别为以上等腰直角三角形的底边,则y1+y2+y3+…+y2019的值等于_____.
(x>0)的图象上,点Q1、Q2、Q3、……、Qn均在x轴的正半轴上,且△OP1Q1、△Q1P2Q2、△Q2P3Q3、…、△Qn﹣1PnQn均为等腰直角三角形,OQ1、Q1Q2、Q2Q3、……、Qn﹣1Qn分别为以上等腰直角三角形的底边,则y1+y2+y3+…+y2019的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C坐标(0,4),点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求直线AD的函数表达式;
(2)当S=![]() 时,请直接写出t的值;
时,请直接写出t的值;
(3)如果点M是(2)中的直线1上的点,点N在x轴上,并且以A,D,M,N为顶点的四边形是平行四边形,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了检验甲、乙两个车间生产的同一款产品的质量情况,进行了抽样调查,请补充完整.
收集数据 从甲、乙两个车间各随机抽取20个样品,进行了检测,检测结果(单位:mm)如下:
甲车间 | 168 | 175 | 180 | 185 | 172 | 189 | 185 | 182 | 185 | 174 |
192 | 180 | 185 | 178 | 173 | 185 | 169 | 187 | 176 | 180 | |
乙车间 | 186 | 180 | 189 | 183 | 176 | 173 | 178 | 167 | 180 | 175 |
178 | 182 | 180 | 179 | 185 | 180 | 184 | 182 | 180 | 183 |
整理、描述数据 按如下分段整理、描述这两组样本数据:
165.5-170.5 | 170.5-175.5 | 175.5-180.5 | 180.5-185.5 | 185.5-190.5 | 190.5-195.5 | |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 |
(说明:尺寸范围为176mm~190mm的产品为合格)
分析数据 两组样本数据的平均数、众数、中位数、方差如下表所示:
平均数 | 众数 | 中位数 | 方差 | |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
得出结论
(1)补全上列表格;
(2)若乙车间生产1000个该款产品,估计其中合格产品约有 个;
(3)可以推断出 车间生产的该款产品更好,理由为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元![]() .在乙店价格为5元
.在乙店价格为5元![]() ,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为
,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为![]() (
(![]() ).
).
(1)根据题意填表:
一次购买数量∕ | 1.5 | 2 | 3.5 | 6 | … |
在甲店花费∕元 | 6.75 | 15.75 | … | ||
在乙店花费∕元 | 7.5 | 16 | … |
(2)设在甲店花费![]() 元,在乙店花费
元,在乙店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
① 若小明在甲店和在乙店一次购买种子的数量相同,且花费相同,则他在同一个店一次购买种子的数量为 ![]() ;
;
② 若小明在同一个店一次购买种子的数量为3kg,则他在甲、乙两个店中的 店购买花费;
③ 若小明在同一个店一次购买种子花费了45元,则他在甲、乙两个店中的 店购买数量多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com