
 =0,那么菱形的面积等于 .
=0,那么菱形的面积等于 . 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源:不详 题型:解答题
 ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,连接
,连接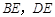 ,其中
,其中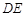 交直线
交直线 于点
于点 .
. ,求
,求 的度数;
的度数; ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 . 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
. 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG. =45°,AB =2,AE=
=45°,AB =2,AE= ,求点G到BE的距离.
,求点G到BE的距离.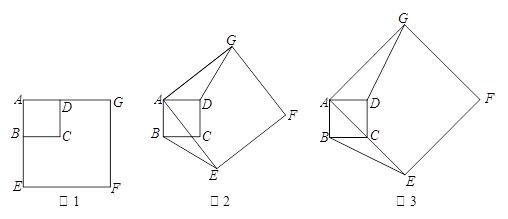
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,AG=1,则EB= .
,AG=1,则EB= .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com