
分析 (1)首先根据选手两次游戏得分超过100分时被“爆掉”,求出甲第二次可取的数有多少;然后根据概率公式,求出甲本轮游戏不被“爆掉”的概率是多少即可.
(2)乙有可能赢.首先根据选手两次游戏得分超过100分时被“爆掉”,求出乙第二次可取的数有多少;然后根据概率公式,求出乙赢的概率是多少即可.
(3)甲选择不转第二次.理由是:甲选择不转第二次,乙必须选择旋转第二次,根据概率公式,求出乙获胜的可能性是多少,可得乙获胜的可能性较小.
解答 解:(1)∵选手两次游戏得分超过100分时被“爆掉”,
∴甲第二次可取5、10、15、20、25、30、35,
∴P(甲不被爆掉)=$\frac{7}{20}$.
(2)乙有可能赢.
∵选手两次游戏得分超过100分时被“爆掉”,
∴乙第二次可取5、10、15,
∴P(乙赢)=$\frac{3}{20}$.
(3)甲选择不转第二次.
理由是:甲选择不转第二次,乙必须选择旋转第二次,
∵选手两次游戏得分超过100分时被“爆掉”,
∴乙获胜的话,第二次可取25、30、35,
此时P(乙赢)=$\frac{3}{20}$,
∴乙获胜的可能性较小.
点评 此题主要考查了概率公式的应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±$\root{3}{a+1}$ | B. | $\root{3}{{{{(x+1)}^2}}}$ | C. | $\root{3}{{{x^2}+1}}$ | D. | ±$\root{3}{{{x^2}+1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
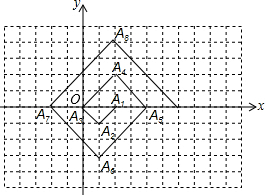 如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).
如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com