
【题目】如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上一点,满足CF⊥CP,过点B作BM⊥CF,分别交AC、CF于点M、N
(1)若AC=![]() AP,AC=4
AP,AC=4![]() ,求△ACP的面积;
,求△ACP的面积;
(2)若BC=MC,证明:CP﹣BM=2FN.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由正方形的性质得出AD=CD=5,∠ADC =90°,根据勾股定理以及AC的长可求得AD=CD=4,再根据AC=![]() AP求出AP长,即可求出S△ACP;
AP求出AP长,即可求出S△ACP;
(2)在CF上截取FN=NG,连接BG,由已知可证得△BCF≌△DCP,可得CF=CP,继而可证得△BCG≌△ABM,可得BM=CG,结合图形即可推导得出CP﹣BM=2FN.
(1)∵四边形ABC是正方形,
∴AD= CD,∠ADC =90°,
∴AC=![]() ,
,
∵AC=4![]() ,
,
∴AD=CD=4,
∵AC=![]() AP,
AP,
∴AP=![]() ,
,
∴S△ACP=![]() AP×CD
AP×CD
=![]() ×
×![]() ×4
×4
=7![]() ;
;
(2)在CF上截取FN=NG,连接BG,
∵四边形ABCD是正方形,
∴AB=CB=CD,
∠CBF=∠CDP=∠BCF+∠FCD=90°,
又∵CF⊥CP,
∴∠DCP+∠FCD=90°,
∴∠BCF=∠BCD,
在△BCF和△DCP中,
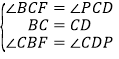 ,
,
∴△BCF≌△DCP,
∴CF=CP,
∵BC=MC,BM⊥CF,
∴∠BCF=∠ACF=![]() ∠BCA=22.5°,
∠BCA=22.5°,
∴∠CFB=67.5°,
∵FC⊥BM,FN=NG,
∴BF=BG,
∴∠FBG=45°,∠FBN=22.5°,
∴∠CBG=45°,
在△BCG和△BAN中,
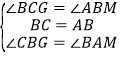 ,
,
∴△BCG≌△ABM,
∴BM=CG,
∴CF﹣CG=FG,
∵BF=BG,BM⊥CF,
∴FN=NG,
∴CP﹣BM=2FN.


科目:初中数学 来源: 题型:
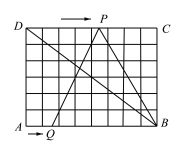
【题目】如图,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.运动时间t 为_______秒时,△PQB成为以PQ为腰的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() —
—![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动,点
运动,点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() -
-![]() 以每秒3个单位长度的速度向终点
以每秒3个单位长度的速度向终点![]() 运动,
运动,![]() 、
、![]() 两点同时出发.分别过
两点同时出发.分别过![]() 、
、![]() 两点作
两点作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).

(1)当![]() 、
、![]() 两点相遇时,求
两点相遇时,求![]() 的值.
的值.
(2)在整个运动过程中,求![]() 的长(用含
的长(用含![]() 的代数式表示).
的代数式表示).
(3)当![]() 与
与![]() 全等时,直接写出所有满足条件的
全等时,直接写出所有满足条件的![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A地在C、B两地之间,甲乙两人分别从A、B两地同时出发,相向而行,经过一段时间后相遇,甲继续向B地前进,乙继续向A地前进;甲到达B地后立即返回,在C地甲追上乙.甲乙两人相距的路程y(米)与出发的时间x(分钟)之间的关系如图所示,则A、C两地相距___米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果,所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算F,规定:F(x,y)=(mx+ny)(3x﹣y)(其中m,n均为非零常数).例如:F(1,1)=2m+2n,F(﹣1,0)=3m.
(1)已知F(1,﹣1)=﹣8,F(1,2)=13.
①求m,n的值;
②关于a的不等式组![]() ,求a的取值范围;
,求a的取值范围;
(2)当x2≠y2时,F(x,y)=F(y,x)对任意有理数x,y都成立,请直接写出m,n满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐城市初级中学为了缓解校门口的交通堵塞,倡导学生步行上学. 小丽步行从家去学校,图中的线段表示小丽步行的路程s(米)与所用时间t(分钟)之间的函数关系. 试根据函数图像回答下列问题:

(1)小丽家离学校 米;
(2)小丽步行的速度是 米/分钟;
(3)求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com