【题目】如图，在中，，，.点从点出发，沿折线—以每秒1个单位长度的速度向终点运动，点从点出发沿折线－以每秒3个单位长度的速度向终点运动，、两点同时出发.分别过、两点作于，于.设点的运动时间为（秒）.

（1）当、两点相遇时，求的值.

（2）在整个运动过程中，求的长（用含的代数式表示）.

（3）当与全等时，直接写出所有满足条件的的长.

参考答案：

【答案】（1）（2）答案不唯一，具体见解析（3）5或或6

【解析】

(1)当P、Q两点相遇时，P点运动距离与A点运动距离的和为AC与BC的长度和，进而可以列出方程，解出t即可；

(2)当点P在AC上时，即时，AP=t，可得PC=6-t，当点P在BC上时，AC+CP=t，此时CP=t-6;

(3)根据点P、Q运动的位置，与全等时有四种情况：①点P在AC上时，点Q在BC上，即；②当点P、点Q都在AC上时，即；③当点P在BC上，点Q在AC上时；④当点P在BC上，点Q在点A处时，即.在这四种情况下将CP与CQ的用t的式子表示出来，利用与全等，可得CP=CQ，可列出关于t的一元二次方程，解出t即可.

解：（1）由题意得:

，

∴，

∴的值为.

（2）当时，．

当时，．

（3）当点P运动t秒时，与全等，有以下四种情况：

①点P在AC上时，点Q在BC上，即，如图所示：

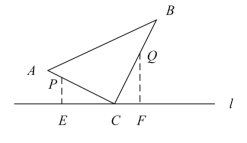
此时CP=6-t，CQ=8-3t，则

6-t=8-3t.

解得：t=1,

此时CQ=8-3×1=5;

②当点P、点Q都在AC上时，即，如图所示：

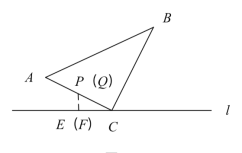
此时AP=t=14-3t,解得：t=,

此时CQ=6-=；

③当点P在BC上，点Q在AC上时，如图所示：

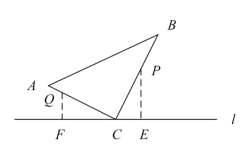
此时无满足条件的t,

因为当点P运动到BC上时，，

此时点Q已经与点A重合；

④当点P在BC上，点Q在点A处时，即，如图所示：

此时CQ=CA=6,CP=t-6，

则6=t-6,解得：t=12，

此时CQ=6.

综上所述，t的值为5或或6.

关闭