Question

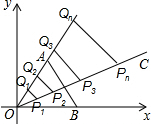
12．如图，在直角坐标系xOy中，点A在第一象限，点B在x轴的正半轴上，△AOB为正三角形，射线OC⊥AB，在OC上依次截取点P₁，P₂，P₃，…，P_n，使OP₁=1，P₁P₂=3，P₂P₃=5，…，P_n-1P_n=2n-1（n为正整数），分别过点P₁，P₂，P₃，…，P_n向射线OA作垂线段，垂足分别为点Q₁，Q₂，Q₃，…，Q_n，则点Q_n的坐标为（$\frac{\sqrt{3}}{4}$n²，$\frac{3}{4}$n²）．

Answer 1

分析 利用特殊直角三角形求出OP_n的值，再利用∠AOB=60°即可求出点Q_n的坐标．

解答 解：∵△AOB为正三角形，射线OC⊥AB，
∴∠AOC=30°，
又∵P_n-1P_n=2n-1，P_nQ_n⊥OA，
∴OQ_n=$\frac{\sqrt{3}}{2}$（OP₁+P₁P₂+P₂P₃+…+P_n-1P_n）=$\frac{\sqrt{3}}{2}$（1+3+5+…+2n-1）=$\frac{\sqrt{3}}{2}$n²，
∴Q_n的坐标为（$\frac{\sqrt{3}}{2}$n²•cos60°，$\frac{\sqrt{3}}{2}$n²•sin60°），
∴Q_n的坐标为（$\frac{\sqrt{3}}{4}$n²，$\frac{3}{4}$n²）．
故答案为：（$\frac{\sqrt{3}}{4}$n²，$\frac{3}{4}$n²）．

点评 本题主要考查了坐标与图形性质，解题的关键是正确的求出OQ_n的值．