
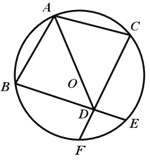
【题目】已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.
(1)求证:BD=CD:
(2)如果AB2=AO·AD,求证:四边形ABDC是菱形.
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】金堂三溪镇被中国柑桔研究所誉为“中国脐橙第一乡”,2016年12月某公司到三溪镇以2.5元/千克购得脐橙12000千克,这些脐橙的销售期最多还有60天,60天后库存的脐橙不能再销售,需要当垃圾处理,处理费为0.1元/千克,经测算,脐橙的销售价格定为8元/千克时,每天可售出100千克;销售单价每降低0.5元,每天可多售出50千克.
(1).如果按8元/千克的价格销售,能否在60天内售完?这些脐橙按此价格销售,获得的利润是多少?
(2).如果按6元/千克的价格销售,这些脐橙获得的利润是多少?当这些脐橙销售价格定为x(![]() )元/千克时,可以使公司每天获得利润最大,每天的最大利润为多少?
)元/千克时,可以使公司每天获得利润最大,每天的最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
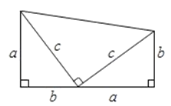
(理解):(1)如图,两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2,![]() 行
行![]() 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:
列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:![]() ________;
________;

(运用):(3)![]() 边形有
边形有![]() 个顶点,在它的内部再画
个顶点,在它的内部再画![]() 个点,以(
个点,以(![]() )个点为顶点,把
)个点为顶点,把![]() 边形剪成若干个三角形,设最多可以剪得
边形剪成若干个三角形,设最多可以剪得![]() 个这样的三角形.当
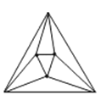
个这样的三角形.当![]() ,
,![]() 时,如图,最多可以剪得
时,如图,最多可以剪得![]() 个这样的三角形,所以
个这样的三角形,所以![]() .
.
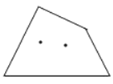
①当![]() ,
,![]() 时,如图,
时,如图,![]() ;当
;当![]() ,
,![]() 时,
时,![]() ;
;
②对于一般的情形,在![]() 边形内画
边形内画![]() 个点,通过归纳猜想,可得
个点,通过归纳猜想,可得![]() (用含
(用含![]() 、
、![]() 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
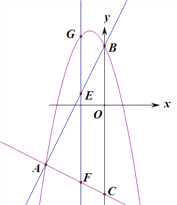
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
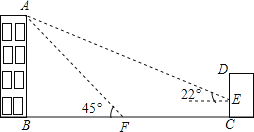
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班班长统计去年1-8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
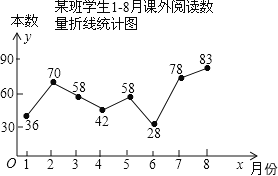
A. 平均数是58B. 众数是42
C. 中位数是58D. 每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
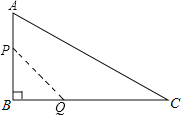
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校数学兴趣小组利用机器人开展数学活动.在相距![]() 个单位长度的直线跑道
个单位长度的直线跑道![]() 上,机器人甲从端点
上,机器人甲从端点![]() 出发,匀速往返于端点
出发,匀速往返于端点![]() 、
、![]() 之间,机器人乙同时从端点
之间,机器人乙同时从端点![]() 出发,以大于甲的速度匀速往返于端点
出发,以大于甲的速度匀速往返于端点![]() 、
、![]() 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
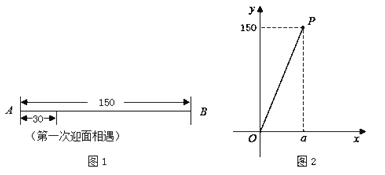
(观察)
①观察图![]() ,若这两个机器人第一次迎面相遇时,相遇地点与点
,若这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,则他们第二次迎面相遇时,相遇地点与点
个单位长度,则他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为 _____个单位长度;
之间的距离为 _____个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,则他们第二次迎面相遇时,相遇地点与点
个单位长度,则他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为 _____个单位长度;
之间的距离为 _____个单位长度;
(发现)
设这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,他们第二次迎面相遇时,相遇地点与点
个单位长度,他们第二次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度.兴趣小组成员发现了
个单位长度.兴趣小组成员发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图
,如图![]() 所示).
所示).
①![]() = _____;
= _____;
②分别求出各部分图象对应的函数表达式,并在图![]() 中补全函数图象;
中补全函数图象;
(拓展)
设这两个机器人第一次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度,他们第三次迎面相遇时,相遇地点与点
个单位长度,他们第三次迎面相遇时,相遇地点与点![]() 之间的距离为
之间的距离为![]() 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点
个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点![]() 之间的距离
之间的距离![]() 不超过
不超过![]() 个单位长度,则他们第一次迎面相遇时,相遇地点与点
个单位长度,则他们第一次迎面相遇时,相遇地点与点![]() 之间的距离
之间的距离![]() 的取值范围是 _____.(直接写出结果)
的取值范围是 _____.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com