
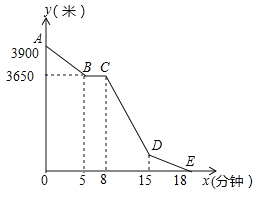
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( ) 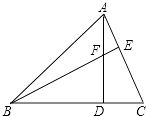
A.40°
B.45°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
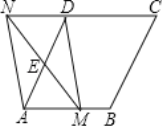
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系式中,正确的是( )
A.(a+b)2=a2﹣2ab+b2
B.(a﹣b)2=a2﹣b2
C.(a+b)2=a2+b2
D.(a+b)(a﹣b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式:
(1)(﹣2)0+( ![]() )﹣2﹣(﹣0.5)201622017
)﹣2﹣(﹣0.5)201622017
(2)先化简,再求值:(a+b)(a﹣b)+(a+b)2﹣2a2 , 其中a=2017,b=﹣ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com