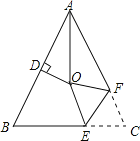
【题目】如图，在
中，
，
，
的平分线与AB的垂直平分线交于点O，将
沿EF折叠，若点C与点O恰好重合，则
______．
【答案】
【解析】
连接OB、OC，根据角平分线的定义求出∠BAO，根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB，根据等边对等角可得∠ABO=∠BAO，再求出∠OBC，然后判断出点O是△ABC的外心，根据三角形外心的性质可得OB=OC，再根据等边对等角求出∠OCB=∠OBC，根据翻折的性质可得OE=CE，然后根据等边对等角求出∠COE，再利用三角形的内角和定理列式计算即可
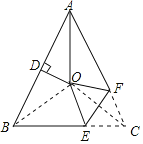
解：如图，连接OB、OC，
，AO为
的平分线，
，
又
，
，
是AB的垂直平分线，
，
，
，
为的平分线，
，
，
点O在BC的垂直平分线上，
又是AB的垂直平分线，
点O是
的外心，
,
，
将
沿
在BC上，F在AC上
折叠，点C与点O恰好重合，
，
，
在
中，
．
故答案为：104°.
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：
【题目】原题呈现：若a2+b2+4a﹣2b+5＝0，求a、b的值．
方法介绍：
①看到a2+4a可想到如果添上常数4恰好就是a2+4a+4＝（a+2）2，这个过程叫做“配方”，同理b2﹣2b+1＝（b﹣1）2，恰好把常数5分配完；
②从而原式可以化为（a+2）2+（b﹣1）2＝0由平方的非负性可得a+2＝0且b﹣1＝0．
经验运用：
（1）若4a2+b2﹣20a+6b+34＝0，求a+b的值．
（2）若a2+5b2+c2﹣2ab﹣4b+6c+10＝0，求a+b+c的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
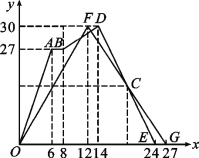
【题目】甲、乙两组同学玩“两人背夹球”比赛，即：每组两名同学用背部夹着球跑完规定的路程，若途中球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲组两位同学掉了球；乙组两位同学顺利跑完．设比赛中同学距出发点的距离用y表示，单位是米；比赛时间用x表示，单位是秒．两组同学比赛过程用图像表示如下：
(1)这是一次 米的背夹球比赛；
(2)线段 表示甲组两位同学在比赛中途掉球，耽误了 秒；
(3)甲组同学到达终点用了 秒，乙组同学到达终点用了 秒，获胜的是 组同学；
(4)请直接写出C点坐标，并说明点C的实际意义．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某公司租用两种型号的货车各一辆，分別将产品运往甲市与乙市（运费收费标准如下表），已知该公司到乙市的距离比到甲市的距离远30km，B车的总运费比A车的总运费少1080元．
（1）求这家公司分别到甲、乙两市的距离；
（2）若A，B两车同时从公司出发，其中B车以60km/h的速度匀速驶向乙市，而A车根据路况需要，先以45kmh的速度行驶了3小吋，再以75km/h的速度行驹到达甲市．
①在行驶的途中，经过多少时间，A，B两车到各自目的地的距离正好相等？
②若公司希望B车能与A车同吋到达目的地，B车必须在以60km/h的速度行驶一段时间后提速，若提速后的速度为70km/h（速度从60km/h提速到70km/h的时间忽略不汁），则B车应该在行驶 小时后提速．
查看答案和解析>>
科目：初中数学 来源： 题型：
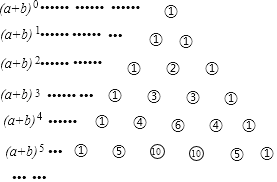
【题目】我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中，用如下的三角形解释(a+b)n的展开式中各项的系数，此三角形称为“杨辉三角”，
即：(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
根据“杨辉三角”计算出(a+b)10的展开式中第三项的系数为( )
A.10B.45C.46D.50
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在“双十二”期间，A，B两个超市开展促销活动，活动方式如下：
A超市：购物金额打9折后，若超过2000元再优惠300元；
B超市：购物金额打8折．
某学校计划购买某品牌的篮球做奖品，该品牌的篮球在A，B两个超市的标价相同．根据商场的活动方式：
（1）若一次性付款4200元购买这种篮球，则在B商场购买的数量比在A商场购买的数量多5个．请求出这种篮球的标价；
（2）学校计划购买100个篮球，请你设计一个购买方案，使所需的费用最少．（直接写出方案）
查看答案和解析>>
科目：初中数学 来源： 题型：
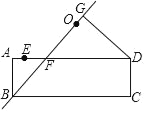
【题目】如图，矩形ABCD中，AB＝3，AD＝9，点E在边AD上，AE＝1，过E、D两点的圆的圆心O在边AD的上方，直线BO交AD于点F，作DG⊥BO，垂足为G．当△ABF与△DFG全等时，⊙O的半径为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小宇想测量位于池塘两端的A，B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到点D处，测得∠BDF=60°．若直线AB与EF之间的距离为60米，求A，B两点的距离．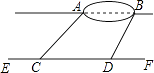
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
