
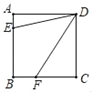
【题目】如图,正方形ABCD的边长为6,点E,F分别在边AB,BC上,若F是BC的中点,且∠EDF=45°,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
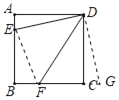
延长F至G,使CG=AE,连接DG,由SAS证明△ADE≌△CDG,得出DE=DG,∠ADE=∠CDG,再证明△EDF≌△GDF,得出EF=GF,设AE=CG=x,则EF=GF=3+x,在Rt△BEF中,由勾股定理得出方程,解方程得出AE=2,在Rt△ADE中,由勾股定理求出DE即可.
解:延长F至G,使CG=AE,连接DG、EF,如图所示:
∵四边形ABCD是正方形,
∴AD=AB=BC=CD=6,∠A=∠B=∠DCF=∠ADC=90°,
∴∠DCG=90°,
在△ADE和△CDG中,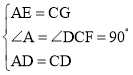 ,
,
∴△ADE≌△CDG(SAS),
∴DE=DG,∠ADE=∠CDG,
∴∠EDG=∠CDE+∠CDG=∠CDE+∠ADE=90°,
∵∠EDF=45°,
∴∠GDF=45°,
在△EDF和△GDF中,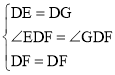 ,
,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵F是BC的中点,
∴BF=CF=3,
设AE=CG=x,则EF=GF=3+x,
在Rt△BEF中,由勾股定理得:32+(6﹣x)2=(3+x)2,
解得:x=2,即AE=2,
在Rt△ADE中,由勾股定理得:DE=![]() ;
;
故选:B.


科目:初中数学 来源: 题型:
【题目】图(a)是正方形纸板制成的一副七巧板.
(1)请你在图(a)中给它的每一小块用①~⑦编号(编号直接标在每一小块对应图形内部的空白处;每小块只能与一个编号对应,每个编号只能和一个小块对应),并同时满足以下三个条件:
条件1:编号为①~③的三小块可以拼成一个轴对称图形;
条件2:编号为④~⑥的三小块可以拼成一个中心对称图形;
条件3:编号为⑦的小块是中心对称图形.
(2)请你在图(b)中画出编号为①~③的三小块拼出的轴对称图形;在图(c)中画出编号为④~⑥的三小块拼出的中心对称图形.(注意:没有编号不得分)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信,这五封信的重量分别是![]() .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
业务种类 | 计费单位 | 资费标准/元 | 挂号费/(元/封) | 特制信封(元/个) |
挂号信 | 首重100g,每重20g | 0.8 | 3 | 0.5 |
续重101~2000g,每重100g | 2.00 | |||
特制信封 | 首重1000g内 | 5.00 | 3 | 1.0 |
(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2)这五封信分别以怎样的方式寄出最合算?请说明理由.
(3)通过解答上述问题,你有何启示?(请你用一两句话说明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
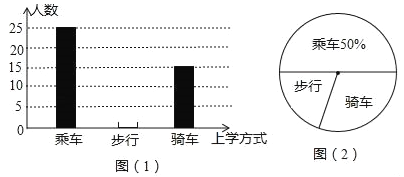
【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)求该班学生的人数;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)如果全年级共600名同学,请你估算全年级步行上学的学生人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
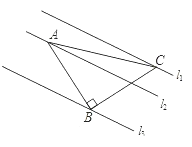
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1、l2之间的距离为2,l2、l3之间的距离为3,则AC的长是_________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定义一种关于n的运算:①当n是奇数时,结果为3n+5②当n为偶数时,结果是![]() (其中k是使
(其中k是使![]() 是奇数的正整数),运算重复进行,如:取n=26,则26
是奇数的正整数),运算重复进行,如:取n=26,则26![]() 13
13![]() 44
44![]() 11……若n=449,则第449次运算的结果是( )
11……若n=449,则第449次运算的结果是( )
A.1B.2C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112-4×2.11×2.22+2.222”,她觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=-1,y=1 | x=1,y=0 | x=3,y=2 | x=2,y=-1 | x=2,y=3 | |
A=2x-y | -3 | 2 | 4 | 5 | 1 |
B=4x2-4xy+y2 | 9 | 4 | 16 |
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请利用A与B之间的关系计算:4×2.112-4×2.11×2.22+2.222.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com