
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为弦,
为弦,![]() ,
,![]() ,
,![]() .
.
![]() 求
求![]() ;
;
![]() 过
过![]() 点作
点作![]() ,交
,交![]() 于
于![]() 点,求
点,求![]() 的值.
的值.

【答案】![]() ;
;![]() .
.
【解析】
(1)作OF⊥DC于F,连结OD,根据垂径定理由OF⊥DC得DF=![]() DC=3.在Rt△ODF中,利用勾股定理可计算出OF=4,然后根据梯形的面积公式计算即可;
DC=3.在Rt△ODF中,利用勾股定理可计算出OF=4,然后根据梯形的面积公式计算即可;
(2)易证四边形ABCD是等腰梯形,作DG⊥AB于G,根据等腰梯形的性质得出DG=OF=4,AG=![]() (AB﹣CD)=2.在Rt△ADG中,由勾股定理得出AD=
(AB﹣CD)=2.在Rt△ADG中,由勾股定理得出AD=![]() =2
=2![]() ,再证明四边形ADCE是平行四边形,得出CE=AD=2
,再证明四边形ADCE是平行四边形,得出CE=AD=2![]() ,AE=CD=6,那么BE=AB﹣AE=4.然后根据S△BCE=
,AE=CD=6,那么BE=AB﹣AE=4.然后根据S△BCE=![]() BCCEsin∠BCE=
BCCEsin∠BCE=![]() BEDG,即可求出sin∠BCE=
BEDG,即可求出sin∠BCE=![]() .
.
(1)作OF⊥DC于F,连结OC,如图,∵OF⊥DC,∴CF=DF=![]() DC=
DC=![]() ×6=3.
×6=3.
∵直径AB=10,∴OD=5.在Rt△ODF中,OF=![]() =4,∴S四边形ABCD=
=4,∴S四边形ABCD=![]() ×(6+10)×4=32;
×(6+10)×4=32;
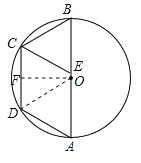
(2)∵CD∥AB,∴![]() =
=![]() ,∴AD=BC.
,∴AD=BC.
∵CD∥AB,CD<AB,∴四边形ABCD是等腰梯形.
作DG⊥AB于G,则DG=OF=4,AG=![]() (AB﹣CD)=2.在Rt△ADG中,由勾股定理得:AD=
(AB﹣CD)=2.在Rt△ADG中,由勾股定理得:AD=![]() =2
=2![]() ,∴BC=AD=2
,∴BC=AD=2![]() .
.
∵CE∥AD,CD∥AB,∴四边形ADCE是平行四边形,∴CE=AD=2![]() ,AE=CD=6,∴BE=AB﹣AE=4.
,AE=CD=6,∴BE=AB﹣AE=4.
∵S△BCE=![]() BCCEsin∠BCE=
BCCEsin∠BCE=![]() BEDG,∴
BEDG,∴![]() ×2
×2![]() ×2
×2![]() sin∠BCE=
sin∠BCE=![]() ×4×4,∴sin∠BCE=
×4×4,∴sin∠BCE=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)求证:AC=CB; (2)若AC=12 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E, F在直线AC上,DF=BE, ∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( )

A.∠D=∠BB.AD=CBC.AE=CFD.AD// BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,高AD和BE交于点H,∠ABC=45°,BE平分∠ABC,下列结论:①∠DAC= 22.5°;②BH= 2CE; ③若连结CH,则CH⊥AB;④若CD=1,则AH=2;其中正确的有( )
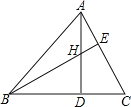
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com