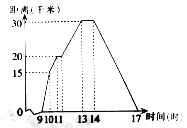
[题目]佳佳某天上午9时骑自行车离开家.17时回家.他有意描绘了离家的距离与时同的变化情况.如图所示.(1)图象表示了哪两个变量的关系?(2)10时和11时.他分别离家多远?(3)他最初到达离家最远的地方是什么时间?离家多远?(4)11时到13时他行驶了多少千米? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】佳佳某天上午9时骑自行车离开家，17时回家，他有意描绘了离家的距离与时同的变化情况，如图所示.

（1）图象表示了哪两个变量的关系？

（2）10时和11时，他分别离家多远？

（3）他最初到达离家最远的地方是什么时间？离家多远？

（4）11时到13时他行驶了多少千米？

【答案】（1）图象表示离家距离与时间之间的关系；（2）10时和11时，他分别离家15千米、20千米；（3）他最初到达离家最远的地方是13时，离家30千米；（4）11时到13时他行驶了10千米．

【解析】

（1）根据函数图像的变量之间关系即可写出；

（2）在函数图像直接可以看出；

（3）在函数图像直接可以看出；

（4）在函数图像得到数据进行计算即可.

解：（1）图象表示离家距离与时间之间的关系；

（2）10时和11时，他分别离家15千米、20千米；

（3）他最初到达离家最远的地方是13时，离家30千米；

（4）11时到13时他行驶了：千米．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】（1）如图，在直线MN上求作一点P，使点P到射线OA和OB的距离相等．（要求用尺规作图，保留作图痕迹，不必写作法和证明过程）

（2）等腰三角形的两边长满足|a－4|＋(b－9)2＝0.求这个等腰三角形的周长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】画图并填空：

如图，△ABC的顶点都在方格纸的格点上，将△ABC向下平移2倍，再向右平移3格．

（1）请在图中画出平移后的△A′B′C′；

（2）在图中画出△的A′B′C′的高C′D′（标出点D′的位置）；

（3）如果每个小正方形边长为1，则△A′B′C′的面积=　　　．（答案直接填在题中横线上）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求证：CD⊥AB

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知直线l1∥l2，直线l3和直线l1，l2交于点C和D，直线l3上有一点P。

（1）如图1，若P点在C，D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化，并说明理由；

（2）若点P在C，D两点的外侧运动时(P点与点C，D不重合，如图2和3)，试写出∠PAC，∠APB，∠PBD之间的关系，并说明理由。（图3只写结论，不写理由）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:(1) 当x= -2时,y=1;(2) 当x> x2时,y>0;(3)方程kx2+(2k-1)x-1=0有两个不相等的实数根x1,x2;(4) x1<-1,x2>-1;(5) x2 -x1 = ,其中正确的结论有_______(只需填写序号)