练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，有一圆柱，其高为12cm，它的底面半径为3cm，在圆柱下底面A处有一只蚂蚁，它想得到上面B处的食物，则蚂蚁经过的最短距离为（　　）cm．（π取3）
    A、12B、15C、14D、18
    考点：平面展开-最短路径问题
    专题：
    分析：先把圆柱的侧面展开得其侧面展开图，则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πr，蚂蚁经过的最短距离为连接A，B的线段长，由勾股定理求得AB的长．
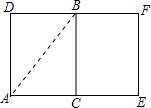    解答：解：如图，将圆柱的侧面沿过A点的一条母线剪开，得到长方形ADFE，
    连接AB，则线段AB的长就是蚂蚁爬行的最短距离，其中C，B分别是AE，DF的中点．
    ∵AD=12cm，DB=πr=3π=9cm（π取3），
    ∴AB=
    		AD2+BD2
    =
    		122+92
    =15cm．
    故选B．
    点评：本题考查平面展开-最短路径问题，解题的关键是计算出圆柱展开后所得长方形的长和宽的值，然后用勾股定理进行计算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在圆O中，圆心O离弦AB距离等于弦长的一半，该弦所对的弧长是47π，求圆O半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一件工作，甲单独做需要20h，乙单独做需要12h，现先由甲单独做4h，若剩下的由甲、乙合作完成，则还需要多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

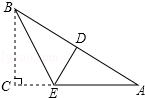    如图，在三角形纸片ABC中，∠C=90°，AC=6，折叠该纸片，使点C落在AB边上的D点处，折痕BE与AC交于点E，若AD=BD，则折痕BE的长为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示圆柱形玻璃容器，高17cm，底面周长为24cm，在外侧下底面点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇，急于捕获苍蝇充饥的蜘蛛，所走的最短路线的长度是（　　）
    A、20cm
    B、8
    		13
    cm
    C、
    		433
    cm
    D、24cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    		2x2-7x+1
    -
    		2x2-9x+4
    =1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知△ABC的顶点坐标为A（3，4）、B（0，0）、C（5，0）．
    （1）以点B为位似中心，把△ABC作位似变换，使△ABC与变换后三角形的位似比是
    5
    12
    ，确定点A、C的对应点的坐标；
    （2）以点D（-1，0）为位似中心，把△ABC作位似变换，使△ABC与变换后的三角形的相似比是
    1
    2
    ，确定点A、C对应点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：0.1253×（-0.25）3×26×（-2）12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，⊙O的直径AB=10cm，∠CBD=45°，求弦CD的长．

    查看答案和解析>>

    同步练习册答案