

分析 (1)根据∠AOC=90°,∠DOC=30°,求出∠AOD的度数,然后即可求出∠AOB的度数;
(2)根据余角的性质可得图(甲)中和∠AOD相等的角;
(3)首先以OB为边,在∠BOC外画∠BOD=90°,再以OC为边在∠COD外画∠AOC=90°,即可得到∠AOD=∠BOC.
解答 解:(1)∵∠AOC=∠DOB=90°,∠DOC=30°,
∴∠AOD=90°-30°=60°,
∴∠AOB=90°+60°=150°.
(2)图(甲)中和∠AOD相等的角是∠BOC,同角的余角相等(或见下面解释)
∵∠AOC=∠DOB=90°,
∴∠AOD+∠DOC=∠BOC+∠DOC,
∴∠AOD=∠BOC;
(3)如图所示:∠AOD=∠BOC.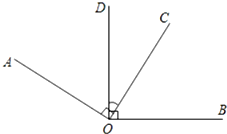
故答案为:150.
点评 本题考查了余角和补角,以及角的计算,解决本题的关键是熟记余角和补角的定义.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:选择题
| A. | (-3x3y3)2=3x6y6 | B. | a10•a2=a20 | ||
| C. | (-m2)5•(-m3)2=m16 | D. | (-$\frac{1}{2}$x2y4)3=-$\frac{1}{8}$x6y12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
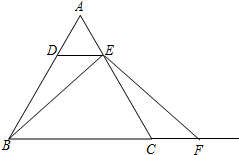 如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B. | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C. | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D. | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
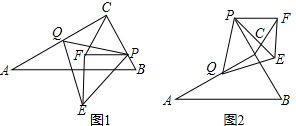
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
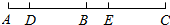 如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.
如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com