
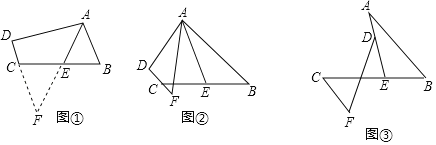
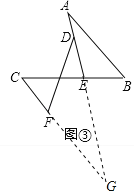
【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
【答案】(1)AD=AB+DC;(2)AB=AF+CF,证明见解析;(3)AB=![]() (CF+DF),证明见解析.
(CF+DF),证明见解析.
【解析】试题分析:(1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;
(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明;
(3)延长AE交CF的延长线于点G,根据相似三角形的判定定理得到△AEB∽△GEC,根据相似三角形的性质得到AB=![]() CG,计算即可.
CG,计算即可.
试题解析:(1)如图①,延长AE交DC的延长线于点F,
∵AB∥DC,∴∠BAF=∠F,
∵E是BC的中点,∴CE=BE,
在△AEB和△FEC中, 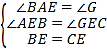 ,∴△AEB≌△FEC,∴AB=FC,
,∴△AEB≌△FEC,∴AB=FC,
∵AE是∠BAD的平分线,∴∠DAF=∠BAF,∴∠DAF=∠F,∴DF=AD,∴AD=DC+CF=DC+AB,
故答案为:AD=AB+DC;
(2)AB=AF+CF,
证明如下:如图②,延长AE交DF的延长线于点G,
∵E是BC的中点,∴CE=BE,
∵AB∥DC,∴∠BAE=∠G,
在△AEB和△GEC中, 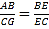 ,∴△AEB≌△GEC,∴AB=GC,
,∴△AEB≌△GEC,∴AB=GC,
∵AE是∠BAF的平分线,∴∠BAG=∠FAG,
∵AB∥CD,∴∠BAG=∠G,∴∠FAG=∠G,∴FA=FG,∴AB=CG=AF+CF;
(3)AB=![]() (CF+DF),
(CF+DF),
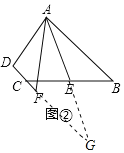
证明如下:如图③,延长AE交CF的延长线于点G,
∵AB∥CF,∴△AEB∽△GEC,∴![]() =
=![]() ,即AB=
,即AB=![]() CG,
CG,
∵AB∥CF,∴∠A=∠G,
∵∠EDF=∠BAE,∴∠FDG=∠G,∴FD=FG,∴AB=![]() CG=
CG=![]() (CF+DF).
(CF+DF).


科目:初中数学 来源: 题型:
【题目】从如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填在表示它所在的集合里:
12,![]() ,
,![]() ,
,![]() ,
,![]()
(1)正数集合:{ }; (2)负数集合:{ };
(3)整数集合;{ }; (4)分数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
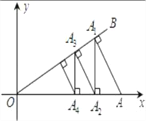
【题目】如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;
过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂
足为点A4…;这样一直作下去,则A2018的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本![]() (单位:元)、销售价
(单位:元)、销售价![]() (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
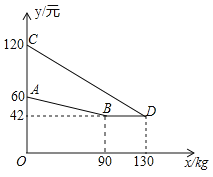
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() 点表示数
点表示数![]() 点表示数
点表示数![]() 是最小的正整数,且
是最小的正整数,且![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)若将数轴折叠,使![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数_______表示的点重合;
与数_______表示的点重合;
(3)点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度在数轴上向点
个单位长度的速度在数轴上向点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 后立即返回,仍然以每秒
后立即返回,仍然以每秒![]() 个单位长度的速度运动至
个单位长度的速度运动至![]() 点停止,设运动时间为
点停止,设运动时间为![]()
①当![]() 时,求点
时,求点![]() 表示的有理数;
表示的有理数;
②当点![]() 表示的有理数与
表示的有理数与![]() 点的距离为
点的距离为![]() 个单位长度时,直接写出所有满足条件的
个单位长度时,直接写出所有满足条件的![]() 值.
值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店出售网球和网球拍,网球拍每只定价80元,网球每个定价4元,商家为促销商品,同时向客户提供两种优惠方案:①买一只网球拍送3个网球:②网球拍和网球都按定价的9折优惠,现在某客户要到该商店购买球拍20只,网球![]() 个(
个(![]() 大于20).
大于20).
(1)若该客户按优惠方案①购买需付款多少元?(用含![]() 的式子表示)
的式子表示)
(2)若该客户按优惠方案②购买需付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)若![]() 时,通过计算说明,此时按哪种优惠方案购买较为合算?
时,通过计算说明,此时按哪种优惠方案购买较为合算?
(4)当![]() 时,你能结合两种优惠方案给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出所需的钱数.
时,你能结合两种优惠方案给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出所需的钱数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com