
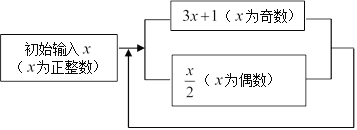
【题目】在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.
如,当初始输入5时,即![]() =5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…
=5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…
(1)当初始输入1时,第1次计算结果为 ;
(2)当初始输入4时,第3次计算结果为 ;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
【答案】(1)4;(2)4;(3)7,4.
【解析】
(1)输入数1是奇数,按照计算程序代入3x+1求结果;
(2)输入数4是偶数,代入![]() 计算得2,将x=2作为输入数代入
计算得2,将x=2作为输入数代入![]() 计算得1,再将x=1代入3x+1计算,即为输出结果;
计算得1,再将x=1代入3x+1计算,即为输出结果;
(3)输入数3,依次代入计算,观察结果,得到结果的规律,即可得到第20次计算结果.
(1)当x=1时,第1次输出结果为:3x+1=4,故填:4;
(2)当x=4时,第1次输出结果为:![]() =2,第2次输出结果为:
=2,第2次输出结果为:![]() =1,第3次输出结果为:3x+1=4,故填:4;
=1,第3次输出结果为:3x+1=4,故填:4;
(3)当x=3时,
第1次输出3x+1=10,
第2次输出![]() =5,
=5,
第3次输出3x+1=16,
第4次输出![]() =8,
=8,
第5次输出![]() =4,
=4,
第6次输出![]() =2,
=2,
第7次输出![]() =1,
=1,
第8次输出3x+1=4,
第9次输出![]() =2,
=2,
可以发现:从第5次开始,结果都是4,2,1三个数循环,
∵![]() ,
,
∴第20次输出的结果为4.


科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() 给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,
给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,![]() ),(2,
),(2,![]() ),都是“同心有理数对”.
),都是“同心有理数对”.
(1)数对(﹣2,1),(3,![]() )是 “同心有理数对”的是__________.
)是 “同心有理数对”的是__________.
(2)若(a,3)是“同心有理数对”,求a的值;
(3)若(m,n)是“同心有理数对”,则(﹣n,﹣m) “同心有理数对”(填“是”或“不是”),说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
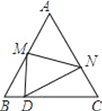
【题目】如图,等边△ABC中,D是边BC上的一点,且BD:DC=3:5,把△ABC折叠,使点A落在边BC上的点D处,若AM=5,那么AN的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
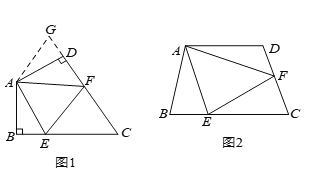
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市要销售一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)求销售单价为多少元时,该文具每天的销售利润最大,并求出最大的利润;
(2)经过试营销后,超市按(1)中单价销售,为了回馈广大顾客,同时提高该文具知名度,超市决定在1月1日当天开展降价促销活动,若每件文具降价2a%,则可多售出4a%,结果当天销售额为5670元,要使销量尽可能地大,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.
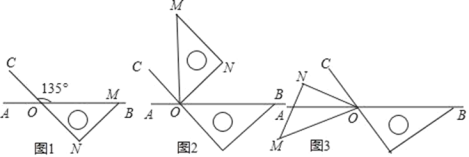
(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM= ;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第 秒时,∠COM与∠CON互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张分别标有数字2,3,4,6的扑克牌,除正面的数字外,牌的形状、大小完全相同.小红先从口袋中随机摸出一张扑克牌并记下牌上的数字为x;小颖在剩下的3张扑克牌中随机摸出一张扑克牌并记下牌上的数字为y,
(1)事件①:小红摸出标有数字3的牌,事件②:小颖摸出标有数字1的牌,则( )
A.事件①是必然事件,事件②是不可能事件,
B.事件①是随机事件,事件②是不可能事件,
C.事件①是必然事件,事件②是随机事件,
D.事件①是随机事件,事件②是必然事件,
(2)若|x-y|≤2,则说明小红与小颖“心领神会”,请求出她们“心领神会”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com