
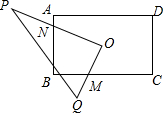
 如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.
如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$. 分析 过点O分别作OF⊥AB与F,OE⊥BC与E,易证明△NOF∽△MOE,利用相似比作为相等关系即可得到关于x,y的方程,整理即可得到函数关系式.
解答 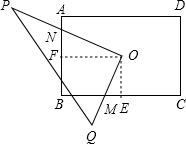 解:过点O分别作OF⊥AB与F,OE⊥BC与E
解:过点O分别作OF⊥AB与F,OE⊥BC与E
∵∠POQ=∠EOF=90°
∴∠NOF=∠MOE
∵∠NFO=∠MEO=90°
∴△NOF∽△MOE
∴$\frac{NF}{OF}=\frac{ME}{OE}$,
∵AB=4,AD=6,BM=x,AN=y
∴NF=2-y,ME=3-x,OF=3,OE=2
∴$\frac{2-y}{3}=\frac{3-x}{2}$
∴y=$\frac{3}{2}$x-$\frac{5}{2}$(0<x<6).
故答案为:y=$\frac{3}{2}$x-$\frac{5}{2}$.
点评 本题考查了相似三角形的判定和性质,求函数的解析式,矩形的性质,正确的作出辅助线是解题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
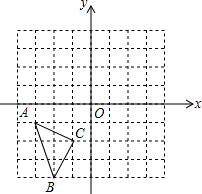 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/袋) | m | m-2 |
| 售价(元/袋) | 20 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com