
����Ŀ����ͼ����֪������C1��y=a(x+2)2-5�Ķ���ΪP����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����B�ĺ�������1��
(1) ��P�����꼰a��ֵ��
(2)��ͼ��1����
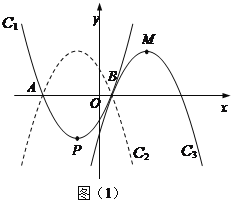
������C2��������C1����x��Գƣ���������C2����ƽ�ƣ�ƽ�ƺ��������ΪC3��C3�Ķ���ΪM������P��M���ڵ�B�����ĶԳ�ʱ����C3�Ľ���ʽ��
(3) ��ͼ��2����
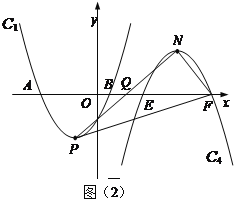
��Q��x����������һ�㣬��������C1�Ƶ�Q��ת180����õ�������C4��������C4�Ķ���ΪN����x���ཻ��E��F���㣨��E�ڵ�F����ߣ������Ե�P��N��FΪ�������������ֱ��������ʱ�����Q�����꣮
���𰸡���1������P��Ϊ��-2��-5����a��![]()
��2��������C3�ı���ʽΪ y=-![]() (x-4)2+5
(x-4)2+5
��3����Q��������![]() ��0����
��0����![]() ��0��ʱ���Ե�P��N��FΪ����
��0��ʱ���Ե�P��N��FΪ����
����������ֱ�������Σ�
��������
(1)��B��1,0������y=a(x+2)2-5�����ɽ��aֵ��
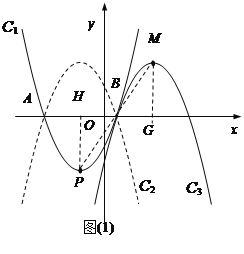
��2������PM����PH��x����H����MG��x����G,����P��M���ڵ�B�����ĶԳƣ�֤����PBH�ա�MBG���������MG��PH��5��BG��BH��3���õ�����M�����꣬�ٸ���������C2��C1����x��ԳƵõ���������C3��C2ƽ�Ƶõ�������д��������C3�ı���ʽ
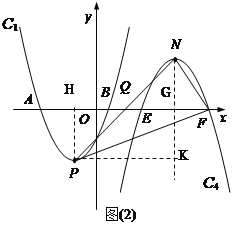
��3������������C4��C1�Ƶ�x���ϵĵ�Q��ת180���õ�����N��������Ϊ5�����N������Ϊ��m,5������PH��x����H����NG��x����G����PK��NG��K�������EF��AB��2BH��6��FG��3����F����Ϊ��m+3��0����H����Ϊ��2��0����K����Ϊ��m��-5����
���ݹ��ɶ�����PN2��NK2+PK2��m2+4m+104��PF2��PH2+HF2��m2+10m+50��NF2��52+32��34���ٷ�����������ۼ���.
(1)��������C1��y=a(x+2)2-5����
����P����-2��-5��
����B��1��0����������C1��
��0= a(1+2)2-5
��ã�a��![]()
(2)����PM����PH��x����H����MG��x����G
����P��M���ڵ�B�����ĶԳ�
��PM����B����PB��MB
���PBH�ա�MBG
��MG��PH��5��BG��BH��3
������M��������4��5��
��������C2��C1����x��ԳƵõ���������C3��C2ƽ�Ƶõ�
��������C3�ı���ʽΪ y=-![]() (x-4)2+5
(x-4)2+5
��3����������C4��C1�Ƶ�x���ϵĵ�Q��ת180���õ�
������N��P���ڵ�Q�����ĶԳ�
�ɣ�2���õ�N��������Ϊ5
���N������m��5��
��PH��x����H����NG��x����G����PK��NG��K
����ת����Q��x����
��EF��AB��2BH��6
��FG��3����F������m+3��0����H������2��0/span>����K������m��-5����
���ݹ��ɶ�����
PN2��NK2+PK2��m2+4m+104
PF2��PH2+HF2��m2+10m+50
NF2��52+32��34
������PNF��90ʱ��PN2+ NF2��PF2�����m��![]() ��
��
��Q��������![]() ��0��
��0��
������PFN��90ʱ��PF2+ NF2��PN2�����m��![]() ����Q������Ϊ��
����Q��������![]() ��0��
��0��
�ۡ�PN��NK��10��NF�����NPF��90
�������ã���Q������Ϊ��![]() ��0����
��0����![]() ��0��ʱ���Ե�P��N��FΪ����
��0��ʱ���Ե�P��N��FΪ����
����������ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=16cm��BC=6cm������P��Q�ֱ���3cm/s��2cm/s���ٶȴӵ�A��Cͬʱ��������Q�ӵ�C���D�ƶ���
��1������P�ӵ�A�ƶ�����Bֹͣ����Q���P��ֹͣ��ֹͣ�ƶ�����P��Q�ֱ�ӵ�A��Cͬʱ�������ʾ����ʱ��P��Q����֮��ľ�����10cm��
��2������P����AB��BC��CD�ƶ�����P��Q�ֱ�ӵ�A��Cͬʱ��������Q�ӵ�C�ƶ�����Dֹͣʱ����P���Q��ֹͣ��ֹͣ�ƶ�����̽���ʱ����PBQ�����Ϊ12cm2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺������ʵ��������(x,y)ͬʱ����һ�κ���y=px+q�ͷ���������y=![]() ������κ���y=px2+qxkΪһ�κ����ͷ�������������������������
������κ���y=px2+qxkΪһ�κ����ͷ�������������������������
(1)���ж�(��Ҫд���жϹ���)��һ�κ���y=x+3�ͷ���������y=![]() �Ƿ�����������������������ڣ�д�����ǵ���������������ʵ�������꣮
�Ƿ�����������������������ڣ�д�����ǵ���������������ʵ�������꣮
(2)��֪������m��n��t��������t<n<8m������һ�κ���y=(1+n)x+2m+2�뷴��������y=![]() ����������������y=(m+t)x2+(10mt)x2015����m��ֵ��
����������������y=(m+t)x2+(10mt)x2015����m��ֵ��
(3)��ͬʱ��������ʵ��������[x1,y1]��[x2,y2]ʹһ�κ���y=ax+2b�ͷ���������y=![]() Ϊ�����������������У�ʵ��a>b>c��a+b+c=0����
Ϊ�����������������У�ʵ��a>b>c��a+b+c=0����![]() ����L��ȡֵ��Χ��
����L��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ![]() ��������ABCD�У�G��AD�ӳ����ϵ�һ�㣬��DΪAG�е㣬����M��A���������ÿ��1����λ���ٶ��ؿ�A��C��G��·����G�������˶���M����A��G�غϣ������˶�ʱ��t�룬����BM���ӳ���AG��N�㣮
��������ABCD�У�G��AD�ӳ����ϵ�һ�㣬��DΪAG�е㣬����M��A���������ÿ��1����λ���ٶ��ؿ�A��C��G��·����G�������˶���M����A��G�غϣ������˶�ʱ��t�룬����BM���ӳ���AG��N�㣮
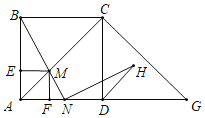
��1����tΪ��ֵʱ����ABMΪ���������Σ�
��2������N��AD����ʱ����DN��HN��NH����CDG��ƽ������H����֤��BN��HN��
��3������M�ֱ���AB��AD�Ĵ��ߣ�����ֱ�ΪE��F������AEMF���ACG�ص����ֵ����ΪS����ֱ��д��S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2 �ǹ���x�ķ��̣�x��2����x��m��=��p��2����p��m��������ʵ������
��1����x1��x2 ��ֵ��
��2����x1��x2 ��ijֱ�������ε���ֱ�DZߵij����ʵ�ʵ��m��p����ʲô����ʱ����ֱ�������ε���������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ����ǰ������Խ��߽�����ı��εĺ�г�ߣ�����ı��ν�����г�ı��Σ������ξ��Ǻ�г�ı��Σ�

��1����ͼ1��������ABCD�У�AD��BC����BAD=120������C=75����BDƽ����ABC����֤��BD������ABCD�ĺ�г�ߣ�
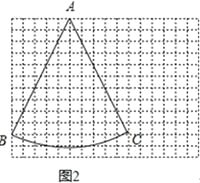
��2����ͼ2����12��16������ͼ�ϣ�ÿ��С�����εı߳�Ϊ1����һ������BAC����A��B��C���ڸ���ϣ����ڴ������������������ͼ�ϸ���һ����D��ʹ����A��B��C��DΪ������ı��ε������Խ��߶��Ǻ�г�ߣ���������Ӧ�ĺ�г�ı��Σ�
��3���ı���ABCD�У�AB=AD=BC����BAD=90����AC���ı���ABCD�ĺ�г�ߣ�����BCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
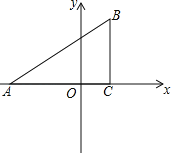
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB��90������A��C������ֱ�ΪA����3��0����C��1��0����BC��![]() AC
AC
��1�������A��B��ֱ�ߵĺ�������ʽ��
��2����x������һ��D������DB��ʹ�á�ADB���ABC���ƣ�������ȫ�ȣ��������D�����ꣻ
��3���ڣ�2���������£���P��Q�ֱ���AB��AD�ϵĶ��㣬����PQ����AP��DQ��m�����Ƿ����������m��ʹ�á�APQ���ADB���ƣ�����ڣ������m��ֵ���粻���ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A����2��0����B��4��0����������y=ax2+bx��1��A��B���㣬�����A���ֱ��y=��![]() x��1���ڵ�C��
x��1���ڵ�C��
��1���������߽���ʽ���Գ��
��2���������ߵĶԳ������Ƿ����һ��P��ʹ�ı���ACPO���ܳ���С�������ڣ������P�����꣬�������ڣ���˵�����ɣ�
��3����MΪy���Ҳ���������һ�㣬����M��ֱ��AC�Ĵ��ߣ�����ΪN���ʣ��Ƿ���������ĵ�N��ʹ�Ե�M��N��CΪ���������������AOC���ƣ������ڣ������N�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
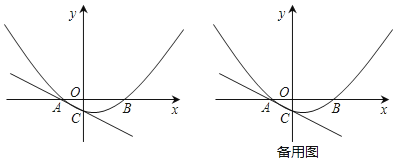
����Ŀ����ͼ�����κ���y��x2��4x+m��ͼ����y�ύ�ڵ�C����B�ǵ�C���ڸö��κ���ͼ��ĶԳ���ԳƵĵ㣮��֪һ�κ���y��kx+b��ͼ���ö��κ���ͼ���ϵ�A��1��0������B��
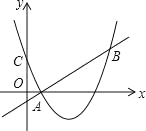
��1������κ�����һ�κ����Ľ���ʽ��
��2������ͼ��ֱ��д������kx+b��x2��4x+m��x��ȡֵ��Χ��
��3���������ߵĶԳ������Ƿ����һ��Pʹ��PA+PC��С����P�����꼰��Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com