
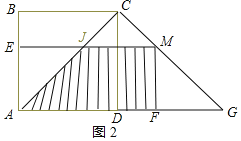
【题目】如图,在边长为![]() 的正方形ABCD中,G是AD延长线上的一点,且D为AG中点,动点M从A点出发,以每秒1个单位的速度沿看A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间t秒,连接BM并延长交AG于N点.
的正方形ABCD中,G是AD延长线上的一点,且D为AG中点,动点M从A点出发,以每秒1个单位的速度沿看A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间t秒,连接BM并延长交AG于N点.
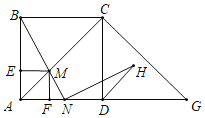
(1)当t为何值时,△ABM为等腰三角形?
(2)当点N在AD边上时,若DN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,请直接写出S的最大值.
【答案】(1)存在;(2)详见解析;(3)当t=![]() 时,S的最大值为
时,S的最大值为![]() .
.
【解析】
(1)四种情况:当点M为AC的中点时,AM=BM;当点M与点C重合时,AB=BM;当点M在AC上,且AM=![]() 时,AM=AB;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;
时,AM=AB;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;
(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;
(3)①当M在AC上时,即0<t≤2时,△AMF为等腰直角三角形,得出AF=FM=![]() t,求出S=
t,求出S=![]() AFFM=
AFFM=![]() t2;当t=2时,即可求出S的最大值;
t2;当t=2时,即可求出S的最大值;
②当M在CG上时,即2<t<4时,先证明△ACD≌△GCD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=![]() t,得出S=S△ACG-S△CMJ-S△FMG,S为t的二次函数,即可求出结果.
t,得出S=S△ACG-S△CMJ-S△FMG,S为t的二次函数,即可求出结果.
(1)解:存在;当点M为AC的中点时,AM=BM,则△ABM为等腰三角形;
当点M与点C重合时,AB=BM,则△ABM为等腰三角形;
当点M在AC上,且AM=![]() 时,AM=AB,则△ABM为等腰三角形;
时,AM=AB,则△ABM为等腰三角形;
当点M为CG的中点时,AM=BM,则△ABM为等腰三角形;
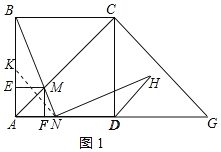
(2)证明:在AB上截取AK=AN,连接KN;如图1所示:
∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∴∠CDG=90°,
∵BK=AB﹣AK,ND=AD﹣AN,
∴BK=DN,
∵DH平分∠CDG,
∴∠CDH=45°,
∴∠NDH=90°+45°=135°,
∴∠BKN=180°﹣∠AKN=135°,
∴∠BKN=∠NDH,
在Rt△ABN中,∠ABN+∠ANB=90°,
又∵BN⊥NH,
即∠BNH=90°,
∴∠ANB+∠DNH=180°﹣∠BNH=90°,
∴∠ABN=∠DNH,
在△BNK和△NHD中,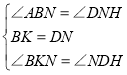 ,
,
∴△BNK≌△NHD(ASA),
∴BN=NH;
(3)解:①当M在AC上时,即0<t≤2时,△AMF为等腰直角三角形,
∵AM=t,
∴AF=FM=![]() t,
t,
∴S=![]() AFFM=
AFFM=![]() ;
;
当t=2时,S的最大值=![]() ×22=1;
×22=1;
②当M在CG上时,即2<t<4时,如图2所示:
CM=t﹣AC=t﹣2,MG=4﹣t,
在△ACD和△GCD中,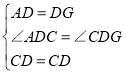 ,
,
∴△ACD≌△GCD(SAS),
∴∠ACD=∠GCD=45°,
∴∠ACM=∠ACD+∠GCD=90°,
∴∠G=90°﹣∠GCD=45°,
∴△MFG为等腰直角三角形,
∴FG=MGcos45°=(4﹣t)![]() =2
=2![]() ﹣
﹣![]() t,
t,
∴S=S△ACG﹣S△CMJ﹣S△FMG=![]() ×2
×2![]() ×
×![]() ﹣
﹣![]() ×CM×CM﹣
×CM×CM﹣![]() ×FM×FG,
×FM×FG,
=2﹣![]() (t﹣2)2﹣
(t﹣2)2﹣![]() (2
(2![]() ﹣
﹣![]() t)2=﹣
t)2=﹣![]() t2+4t﹣4=﹣
t2+4t﹣4=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,S的最大值为
时,S的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 y x2 bx c 的图象与 x 轴交于 A1, 0 、 B 4, 0 两点, 与 y 轴交于点C ,抛物线的对称轴与 x 轴交于点 D ,点 M 从O 点出发,以每秒 1 个单位长度的速度向 B 点运动(运动到 B 点停止),过点 M 作 x 轴的垂线,交抛物线于点 P ,交 BC 与点Q .

(1)求抛物线的解析式;
(2)设当点 M 运动了t (秒)时,四边形OBPC 的面积为 S ,求 S 与t 的函数关系式,并指出自变量t 的取值范围;
(3)在线段 BC 上是否存在点Q ,使得DBQ 成为等腰三角形?若存在,求出点Q 的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+2m2+5,其中y1的图象经过点A(1,1),y3=y1+y2,若y3与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
(1)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,说明理由;
成立?若存在,求出k的值;若不存在,说明理由;
(2)求使![]() ﹣2的值为整数的实数k的整数值;
﹣2的值为整数的实数k的整数值;
(3)若k=﹣2,λ=![]() ,试求λ的值.
,试求λ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
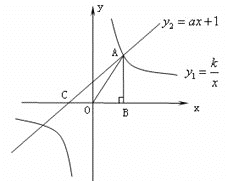
【题目】如图,已知反比例函数![]() 和一次函数
和一次函数![]() 的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
(1)求反比例函数和一次函数的解析式.
(2)若一次函数![]() 的图象与x轴相交于点C,求∠ACO的度数.
的图象与x轴相交于点C,求∠ACO的度数.
(3)结合图象直接写出:当![]() >
>![]() >0时,x的取值范围.
>0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1) 求P点坐标及a的值;
(2)如图(1),
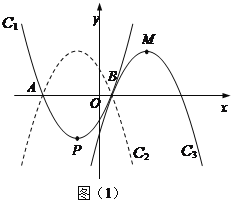
抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3) 如图(2),
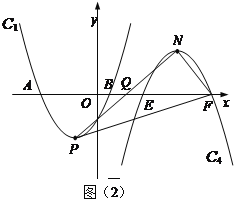
点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
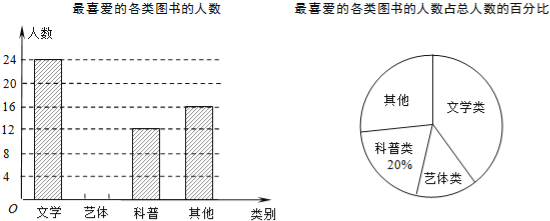
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(﹣3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.
(1)求抛物线的解析式;
(2)连接BE,求h为何值时,△BDE的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com