
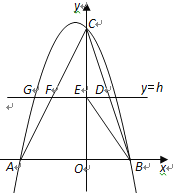
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+6ОЙ§ЕуAЃЈЉ3ЃЌ0ЃЉКЭЕуBЃЈ2ЃЌ0ЃЉЃЎжБЯпy=hЃЈhЮЊГЃЪ§ЃЌЧв0ЃМhЃМ6ЃЉгыBCНЛгкЕуDЃЌгыyжсНЛгкЕуEЃЌгыACНЛгкЕуFЃЌгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгBEЃЌЧѓhЮЊКЮжЕЪБЃЌЁїBDEЕФУцЛ§зюДѓЃЛ
ЃЈ3ЃЉвбжЊвЛЖЈЕуMЃЈЉ2ЃЌ0ЃЉЃЎЮЪЃКЪЧЗёДцдкетбљЕФжБЯпy=hЃЌЪЙЁїOMFЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіhЕФжЕКЭЕуGЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ y=-x2-x+6ЃЎЃЈ2ЃЉ ЕБh=3ЪБЃЌЁїBDEЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() ЃЎЃЈ3ЃЉ ДцдкетбљЕФжБЯпy=2Лђy=4ЃЌЪЙЁїOMFЪЧЕШбќШ§НЧаЮЃЌЕБh=4ЪБЃЌЕуGЕФзјБъЮЊЃЈ-2ЃЌ4ЃЉЃЛЕБh=2ЪБЃЌЕуGЕФзјБъЮЊЃЈ
ЃЎЃЈ3ЃЉ ДцдкетбљЕФжБЯпy=2Лђy=4ЃЌЪЙЁїOMFЪЧЕШбќШ§НЧаЮЃЌЕБh=4ЪБЃЌЕуGЕФзјБъЮЊЃЈ-2ЃЌ4ЃЉЃЛЕБh=2ЪБЃЌЕуGЕФзјБъЮЊЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉАбЕуAЁЂBЕФзјБъЗжБ№ДњШыХзЮяЯпНтЮіЪНЃЌСаГіЙигкЯЕЪ§aЁЂbЕФНтЮіЪНЃЌЭЈЙ§НтЗНГЬзщЧѓЕУЫќУЧЕФжЕМДПЩЕУИУХзЮяЯпЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓЕУЕуCЕФзјБъЃЌдйЧѓЕУжБЯпBCЕФКЏЪ§ЙиЯЕЪНЃЌгУhБэЪОГіDEЕФГЄЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЙЙдьГівдЁїBDEЕФУцЛ§КЭhЮЊБфСПЕФЖўДЮКЏЪ§ФЃаЭЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗжOF=FMЁЂOF=OMКЭFM=OMШ§жжЧщПіЧѓНтМДПЩ.
ЃЈ1ЃЉЁп ХзЮяЯпy=ax2+bx+6ОЙ§ЕуA(-3,0)КЭЕуB(2,0)ЃЌ
Ёр![]()
НтЕУ![]()
Ёр ИУХзЮяЯпЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊy=-x2-x+6.
ЃЈ2ЃЉШчЭМЃЌ
Ёп ХзЮяЯпy=-x2-x+6гыyжсНЛгкЕуCЃЌЁр C(0,6).
ЩшжБЯпBCЕФКЏЪ§ЙиЯЕЪНЮЊy=k1x+b1ЃЌЁр y=-3x+6.
ЕБy=hЪБЃЌ-3x+6=hЃЌЕУ![]() ЃЌМД
ЃЌМД![]() .
.
Ёр ![]() .
.
Ёр ЕБh=3ЪБЃЌЁїBDEЕФУцЛ§зюДѓ.
ЃЈ3ЃЉШчЭМ2.2ЃЌЩшжБЯпACЕФКЏЪ§ЙиЪНЮЊy=k2x+b2ЃЌ
Ёр y=2x+6.
ЕБy=hЪБЃЌ2x+6=hЃЌЕУ![]() ЃЌ
ЃЌ
Ёр F(![]() h-3,h),
h-3,h),
Ёр ![]() .
.
гжЁп M(-2,0)ЃЌ
Ёр OM2=4ЃЌFM2=(![]() h-3+2)2+ h2=(
h-3+2)2+ h2=(![]() h-1)2+ h2.
h-1)2+ h2.
Ђй ШєOF=FMЃЌдђ(![]() h-3)2+ h2=(
h-3)2+ h2=(![]() h-1)2+ h2ЃЌ
h-1)2+ h2ЃЌ
НтЕУh=4.
(СэНтЃКгЩЕШбќШ§НЧаЮЁАШ§ЯпКЯвЛЁБЃЌ
Ёр![]() -3=-1ЃЌЕУh=4.)
-3=-1ЃЌЕУh=4.)
гЩ-x2-x+6=4ЃЌНтЕУx1=-2ЃЌx2=1(ЩсШЅ)ЃЌ
Ёр G(-2,4).
Ђк ШєOF=OMЃЌдђ(![]() h-3)2+ h2=4ЃЌЗНГЬЮоЪЕЪ§Нт.
h-3)2+ h2=4ЃЌЗНГЬЮоЪЕЪ§Нт.
Ђл ШєFM=OMЃЌдђ(![]() h-1)2+ h2=4ЃЌНтЕУh1=2ЃЌ
h-1)2+ h2=4ЃЌНтЕУh1=2ЃЌ![]() (ЩсШЅ).
(ЩсШЅ).
гЩ-x2-x+6=2ЃЌНтЕУ![]() ,
,![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ
ЁрG(![]() ,2).
,2).
злЩЯЫљЪіЃЌДцдкетбљЕФжБЯпy=hЃЌЪЙЁїOFMЪЧЕШбќШ§НЧаЮЃЌДЫЪБh=4ЃЌG(-2,4)Лђh=2ЃЌG(![]() ,2).
,2).



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
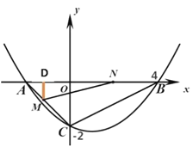
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ![]() ЕФе§ЗНаЮABCDжаЃЌGЪЧADбгГЄЯпЩЯЕФвЛЕуЃЌЧвDЮЊAGжаЕуЃЌЖЏЕуMДгAЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиПДAЁњCЁњGЕФТЗЯпЯђGЕудШЫйдЫЖЏЃЈMВЛгыAЃЌGжиКЯЃЉЃЌЩшдЫЖЏЪБМфtУыЃЌСЌНгBMВЂбгГЄНЛAGгкNЕуЃЎ
ЕФе§ЗНаЮABCDжаЃЌGЪЧADбгГЄЯпЩЯЕФвЛЕуЃЌЧвDЮЊAGжаЕуЃЌЖЏЕуMДгAЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиПДAЁњCЁњGЕФТЗЯпЯђGЕудШЫйдЫЖЏЃЈMВЛгыAЃЌGжиКЯЃЉЃЌЩшдЫЖЏЪБМфtУыЃЌСЌНгBMВЂбгГЄНЛAGгкNЕуЃЎ
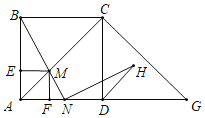
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЁїABMЮЊЕШбќШ§НЧаЮЃП
ЃЈ2ЃЉЕБЕуNдкADБпЩЯЪБЃЌШєDNЁЭHNЃЌNHНЛЁЯCDGЕФЦНЗжЯпгкHЃЌЧѓжЄЃКBNЃНHNЃЛ
ЃЈ3ЃЉЙ§ЕуMЗжБ№зїABЃЌADЕФДЙЯпЃЌДЙзуЗжБ№ЮЊEЃЌFЃЌОиаЮAEMFгыЁїACGжиЕўВПЗжЕФУцЛ§ЮЊSЃЌЧыжБНгаДГіSЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
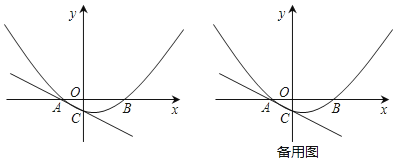
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпy=ax2+bxЉ1Й§AЁЂBСНЕуЃЌВЂгыЙ§AЕуЕФжБЯпy=Љ![]() xЉ1НЛгкЕуCЃЎ
xЉ1НЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАЖдГЦжсЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЫФБпаЮACPOЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуMЮЊyжсгвВрХзЮяЯпЩЯвЛЕуЃЌЙ§ЕуMзїжБЯпACЕФДЙЯпЃЌДЙзуЮЊNЃЎЮЪЃКЪЧЗёДцдкетбљЕФЕуNЃЌЪЙвдЕуMЁЂNЁЂCЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌШєДцдкЃЌЧѓГіЕуNЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
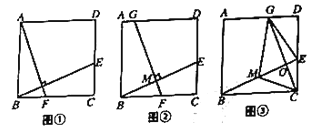
ЁОЬтФПЁПдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧБп
ЪЧБп![]() ЩЯвЛЕуЃЈЕу
ЩЯвЛЕуЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌСЌНс
жиКЯЃЉЃЌСЌНс![]() .ШчЭМЂйЃЌЙ§Еу
.ШчЭМЂйЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .взжЄ
.взжЄ![]() .ЃЈВЛашвЊжЄУїЃЉШчЭМЂкЃЌШЁ
.ЃЈВЛашвЊжЄУїЃЉШчЭМЂкЃЌШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() .
.
ЃЈ2ЃЉСЌНс![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ3ЃЉШчЭМЂлЃЌШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() .Й§Еу
.Й§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЁЂ
ЁЂ![]() .Шє
.Шє![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§.
ЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌгы
ЃЌгы![]() жсЕФСэвЛИіНЛЕуЮЊЕу
жсЕФСэвЛИіНЛЕуЮЊЕу![]() .
.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЭЌЪБЕу
дЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЭЌЪБЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЫйЖШЮЊ2ИіЕЅЮЛГЄЖШ/УыЃЌЕБЕу
дЫЖЏЃЌЫйЖШЮЊ2ИіЕЅЮЛГЄЖШ/УыЃЌЕБЕу![]() ЁЂ
ЁЂ![]() гавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЌСЌНг
гавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЌСЌНг![]() ЃЌЩшдЫЖЏЪБМфЮЊ
ЃЌЩшдЫЖЏЪБМфЮЊ![]() УыЃЌЕБ
УыЃЌЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЕФУцЛ§
ЕФУцЛ§![]() зюДѓЃЌВЂЧѓГі
зюДѓЃЌВЂЧѓГі![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕу![]() дк
дк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() дкХзЮяЯпЩЯЃЌЪЧЗёДцдкЕу
дкХзЮяЯпЩЯЃЌЪЧЗёДцдкЕу![]() ЁЂ
ЁЂ![]() ЃЌЪЙЕУвдЕу
ЃЌЪЙЕУвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу![]() зјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
зјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁКьЕФИИФИПЊСЫвЛИіаЁЗўзАЕъЃЌГіЪлФГжжНјМлЮЊ![]() дЊЕФЗўзАЃЌЯжУПМў
дЊЕФЗўзАЃЌЯжУПМў![]() дЊЃЌУПаЧЦкПЩТє
дЊЃЌУПаЧЦкПЩТє![]() МўЃЎИУЭЌбЇЖдЪаГЁзїСЫШчЯТЕїВщЃКУПНЕМл
МўЃЎИУЭЌбЇЖдЪаГЁзїСЫШчЯТЕїВщЃКУПНЕМл![]() дЊЃЌУПаЧЦкПЩЖрТє
дЊЃЌУПаЧЦкПЩЖрТє![]() МўЃЛУПеЧМл
МўЃЛУПеЧМл![]() дЊЃЌУПаЧЦквЊЩйТє
дЊЃЌУПаЧЦквЊЩйТє![]() МўЃЎ
МўЃЎ
![]() аЁКьвбОЧѓГідкеЧМлЧщПіЯТвЛИіаЧЦкЕФРћШѓ
аЁКьвбОЧѓГідкеЧМлЧщПіЯТвЛИіаЧЦкЕФРћШѓ![]() ЃЈдЊЃЉгыЪлМл
ЃЈдЊЃЉгыЪлМл![]() ЃЈдЊЃЉЃЈ
ЃЈдЊЃЉЃЈ![]() ЮЊећЪ§ЃЉЕФКЏЪ§ЙиЯЕЪНЮЊ
ЮЊећЪ§ЃЉЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЌЧыФуЧѓГідкНЕМлЕФЧщПіЯТ
ЃЌЧыФуЧѓГідкНЕМлЕФЧщПіЯТ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() дкНЕМлЕФЬѕМўЯТЃЌЮЪУПМўЩЬЦЗЕФЪлМлЖЈЮЊЖрЩйЪБЃЌвЛИіаЧЦкЕФРћШѓЧЁКУЮЊ
дкНЕМлЕФЬѕМўЯТЃЌЮЪУПМўЩЬЦЗЕФЪлМлЖЈЮЊЖрЩйЪБЃЌвЛИіаЧЦкЕФРћШѓЧЁКУЮЊ![]() дЊЃП
дЊЃП
![]() ЮЪШчКЮЖЈМлЃЌВХФмЪЙвЛаЧЦкЛёЕУЕФРћШѓзюДѓЃП
ЮЪШчКЮЖЈМлЃЌВХФмЪЙвЛаЧЦкЛёЕУЕФРћШѓзюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНx2Љ4x+mЕФЭМЯѓгыyжсНЛгкЕуCЃЌЕуBЪЧЕуCЙигкИУЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсЖдГЦЕФЕуЃЎвбжЊвЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓОЙ§ИУЖўДЮКЏЪ§ЭМЯѓЩЯЕуAЃЈ1ЃЌ0ЃЉМАЕуBЃЎ
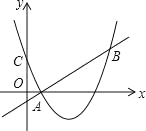
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§гывЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓЃЌжБНгаДГіТњзуkx+bЁнx2Љ4x+mЕФxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуPЪЙЕУPA+PCзюаЁЃЌЧѓPЕузјБъМАзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫСЫНтГѕжаИїФъМЖбЇЩњУПЬьЕФЦНОљЫЏУпЪБМфЃЈЕЅЮЛЃКhЃЌОЋШЗЕН1 hЃЉЃЌГщбљЕїВщСЫВПЗжбЇЩњЃЌВЂгУЕУЕНЕФЪ§ОнЛцжЦСЫЯТУцСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
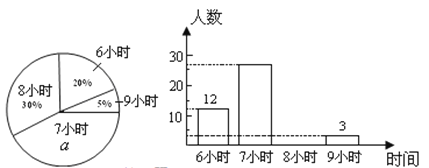
ЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓГіЩШаЮЭГМЦЭМжаАйЗжЪ§![]() ЕФжЕЮЊ_______ЃЌЫљГщВщЕФбЇЩњШЫЪ§ЮЊ______ЃЛ
ЕФжЕЮЊ_______ЃЌЫљГщВщЕФбЇЩњШЫЪ§ЮЊ______ЃЛ
ЃЈ2ЃЉЧѓГіЦНОљЫЏУпЪБМфЮЊ8аЁЪБЕФШЫЪ§ЃЌВЂВЙШЋЬѕаЮЭМЃЛ
ЃЈ3ЃЉЧѓГіетВПЗжбЇЩњЕФЦНОљЫЏУпЪБМфЕФЦНОљЪ§ЃЛ
ЃЈ4ЃЉШчЙћИУаЃЙВгабЇЩњ1200УћЃЌЧыФуЙРМЦЫЏУпВЛзуЃЈЩйгк8аЁЪБЃЉЕФбЇЩњЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
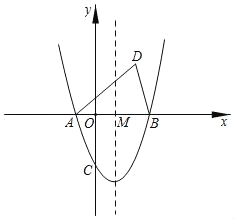
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНx2+bx+cгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌЉ3ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉвбжЊЕуPЃЈmЃЌnЃЉдкХзЮяЯпЩЯЃЌЕБЉ2ЁмmЃМ3ЪБЃЌжБНгаДnЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуMЃЌЕуDгыЕуCЙигкЕуMЖдГЦЃЌЪдЮЪдкИУХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїABPгыЁїABDШЋЕШЃПШєДцдкЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com