
【题目】在正方形![]() 中,
中,![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、
、![]() 重合),连结
重合),连结![]() .如图①,过点
.如图①,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .易证
.易证![]() .(不需要证明)如图②,取
.(不需要证明)如图②,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
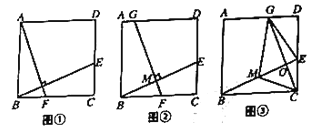
(1)求证:![]() .
.
(2)连结![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
(3)如图③,取![]() 的中点
的中点![]() ,连结
,连结![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)2;(3)4.
【解析】
(1)过点G作GP⊥BC于P,判断出PG=BC,由题目中的材料可知△GPF≌△BCE,即可得出结论;
(2)利用直角三角形斜边上的中线是斜边的一半求解;
(3)借助(1)(2)的结论,结合S四边形GMCE=![]() CG×OE+
CG×OE+![]() CG×OM进行求解即可.
CG×OM进行求解即可.
解:(1)如图②,
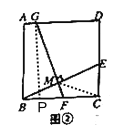
过点G作GP⊥BC于P,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
∴四边形ABPG是矩形,
∴PG=AB,
由题目中的材料可知:△GPF≌△BCE,
∴BE=FG;
(2)由(1)知,BE=FG,连接CM,
∵∠BCE=90°,点M是BE的中点,
∴BE=2CM=2,
∴FG=2;
(3)∵CM=2,
∴ME=2,
由(1)(2)得,CG=BE=4,
∵BE⊥CG,
∴S四边形GMCE=![]() CG×OE+
CG×OE+![]() CG×OM=
CG×OM=![]() CG×ME=
CG×ME=![]() ×4×2=4.
×4×2=4.


科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+2m2+5,其中y1的图象经过点A(1,1),y3=y1+y2,若y3与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
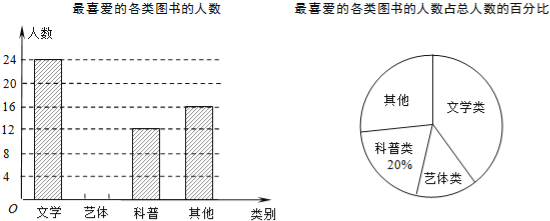
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
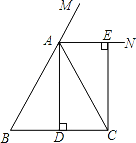
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为兼顾季节性用水差异,大力推进水资源节约,从2019年1月1日起,遵义市中心城区居民生活用水的阶梯水量,将从“月计量”缴费调整为“年计量”缴费按“一户一表”,居民家庭为3口人计算,阶梯用水量及水价见下表:
年用水量(吨) | 水价(元/吨) | |
第一阶梯 | 0~216(含216) |
|
第二阶梯 | 216~288(含288) |
|
第三阶梯 | 288以上 | 8.4 |
小明家和小刚家均为3口之家,2018年全年用水量分别为260吨和300吨,若按“年计量”缴费标准计算,小明家和小刚家全年应缴水费分别为789.6元和1008元.
(1)求表中![]() ,
,![]() 的值;
的值;
(2)小刚家实施节水计划,以2018年用水量为起点,预计2020年用水量降到243吨,且从2018年到2020年每年用水量的平均下降率都相同,请按此下降率计算2021年小刚家用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(﹣3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.
(1)求抛物线的解析式;
(2)连接BE,求h为何值时,△BDE的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
![]() 若一元二次方程
若一元二次方程![]() 有一个根是
有一个根是![]() ,则代数式
,则代数式![]() 的值是
的值是![]()
![]() 若
若![]() ,则
,则![]() 是一元二次方程
是一元二次方程![]() 的一个根
的一个根
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有不相等的两个实数根
有不相等的两个实数根
![]() 当m取整数
当m取整数![]() 或1时,关于x的一元二次方程
或1时,关于x的一元二次方程![]() 与
与![]() 的解都是整数.
的解都是整数.
其中正确的有![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com