
【题目】为兼顾季节性用水差异,大力推进水资源节约,从2019年1月1日起,遵义市中心城区居民生活用水的阶梯水量,将从“月计量”缴费调整为“年计量”缴费按“一户一表”,居民家庭为3口人计算,阶梯用水量及水价见下表:
年用水量(吨) | 水价(元/吨) | |
第一阶梯 | 0~216(含216) |
|
第二阶梯 | 216~288(含288) |
|
第三阶梯 | 288以上 | 8.4 |
小明家和小刚家均为3口之家,2018年全年用水量分别为260吨和300吨,若按“年计量”缴费标准计算,小明家和小刚家全年应缴水费分别为789.6元和1008元.
(1)求表中![]() ,
,![]() 的值;
的值;
(2)小刚家实施节水计划,以2018年用水量为起点,预计2020年用水量降到243吨,且从2018年到2020年每年用水量的平均下降率都相同,请按此下降率计算2021年小刚家用水量.
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
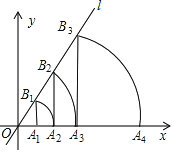
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
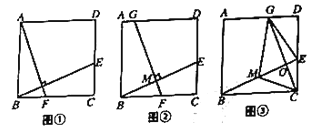
【题目】在正方形![]() 中,
中,![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、
、![]() 重合),连结
重合),连结![]() .如图①,过点
.如图①,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .易证
.易证![]() .(不需要证明)如图②,取
.(不需要证明)如图②,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连结![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
(3)如图③,取![]() 的中点
的中点![]() ,连结
,连结![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=-![]() +bx+c经过A(-1,0)、B(5,0)两点,顶点为P.
+bx+c经过A(-1,0)、B(5,0)两点,顶点为P.
求:(1)求b,c的值;
(2)求△ABP的面积;
(3)若点C(![]() ,
,![]() )和点D(
)和点D(![]() ,
,![]() )在该抛物线上,则当
)在该抛物线上,则当![]() 时,请写出
时,请写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红的父母开了一个小服装店,出售某种进价为![]() 元的服装,现每件
元的服装,现每件![]() 元,每星期可卖
元,每星期可卖![]() 件.该同学对市场作了如下调查:每降价
件.该同学对市场作了如下调查:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件;每涨价
件;每涨价![]() 元,每星期要少卖
元,每星期要少卖![]() 件.
件.
![]() 小红已经求出在涨价情况下一个星期的利润
小红已经求出在涨价情况下一个星期的利润![]() (元)与售价
(元)与售价![]() (元)(
(元)(![]() 为整数)的函数关系式为
为整数)的函数关系式为![]() ,请你求出在降价的情况下
,请你求出在降价的情况下![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为
在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为![]() 元?
元?
![]() 问如何定价,才能使一星期获得的利润最大?
问如何定价,才能使一星期获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连接AC.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连接AC.
(1)求直线AC的解析式;
(2)如图1,点P为直线AC上方抛物线上一动点,过P作PD⊥AB,交AC于点E,点F是线段AC上一动点,连接DF.当△PAC的面积最大时,求DF+![]() AF的最小值;
AF的最小值;
(3)如图2,将△OBC绕着点O顺时针旋转60°得△OB′C′,点G是AC中点,点H为直线OC′上一动点,当△GHB′为等腰三角形时,直接写出对应的点H的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com