
����Ŀ����֪������y����![]() x2��
x2��![]() x+2
x+2![]() ��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C������AC��
��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C������AC��
��1����ֱ��AC�Ľ���ʽ��
��2����ͼ1����PΪֱ��AC�Ϸ���������һ���㣬��P��PD��AB����AC�ڵ�E����F���߶�AC��һ���㣬����DF������PAC��������ʱ����DF+![]() AF����Сֵ��
AF����Сֵ��
��3����ͼ2������OBC���ŵ�O˳ʱ����ת60��á�OB��C�䣬��G��AC�е㣬��HΪֱ��OC����һ���㣬����GHB��Ϊ����������ʱ��ֱ��д����Ӧ�ĵ�H�����꣮

���𰸡���1��ֱ��AC�Ľ���ʽΪy��![]() x+2
x+2![]() ����2����Сֵ
����2����Сֵ![]() ����3����H������Ϊ����2����
����3����H����������2����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����3
����3![]() ��
��![]() ����-3
����-3![]() ��-
��-![]() ����
����
��������
��1���ɩ�![]() x2��
x2��![]() x+2
x+2![]() =0���ֱ����A����6��0����B��2��0��������x��0�����C�����꣬��ֱ��AC�Ľ���ʽΪy��kx+b����A,C��������뼴��.
=0���ֱ����A����6��0����B��2��0��������x��0�����C�����꣬��ֱ��AC�Ľ���ʽΪy��kx+b����A,C��������뼴��.
��2�����P��t����![]() t2��
t2��![]() t+2
t+2![]() ������E��t��
������E��t��![]() ����D��t��0�����ó�PE�������������������ʽ�����������PAC���õ���PAC�������������ù��ɶ������AE, ����D����ֱ��AC�ĶԳƵ�D��
����D��t��0�����ó�PE�������������������ʽ�����������PAC���õ���PAC�������������ù��ɶ������AE, ����D����ֱ��AC�ĶԳƵ�D��![]() ������F��FH��x�ᣬ����Ϊ��H������D����D��K��x�ᣬ����Ϊ��K������D��F���õ�
������F��FH��x�ᣬ����Ϊ��H������D����D��K��x�ᣬ����Ϊ��K������D��F���õ�![]() �����ɽ��.
�����ɽ��.
��3���ȸ����������![]() �����ж���AC��OC�����õ�ֱ��OC���Ľ���ʽΪy��
�����ж���AC��OC�����õ�ֱ��OC���Ľ���ʽΪy��![]() ����H��m��
����H��m��![]() ����������ת�����ʵõ�
����������ת�����ʵõ�![]() ������GHB��Ϊ����������ʱ��
������GHB��Ϊ����������ʱ��
�ٷ���������������ۣ����ɽ��.
��1���ɩ�![]() x2��
x2��![]() x+2
x+2![]() =0��x1����6��x2��2��
=0��x1����6��x2��2��
�ߵ�A�ڵ�B����࣬
��A����6��0����B��2��0����
��x��0����y��2![]() ��
��
��C��0��2![]() ����
����
��ֱ��AC�Ľ���ʽΪy��kx+b��
����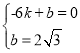 ����ã�
����ã� ��
��
��ֱ��AC�Ľ���ʽΪy��![]() ��
��
��2�����P��t����![]() t2��
t2��![]() t+2
t+2![]() ������E��t��
������E��t��![]() ����D��t��0����
����D��t��0����
��PE����![]() t2��
t2��![]() t+2
t+2![]() -(
-(![]() )����
)����![]() t2��
t2��![]() t��
t��
��![]() ��
��
�൱t����3ʱ����PAC��������ʱP����3��![]() ����E����3��
����E����3��![]() ����D����3��0����
����D����3��0����
��AD����3������6����3��ED��![]() ��
��
��Rt��ADE��AE��![]() ��
��
��ED��![]() ��
��
���EAD��30����
��ͼ������D����ֱ��AC�ĶԳƵ�D��![]() ������F��FH��x�ᣬ
������F��FH��x�ᣬ
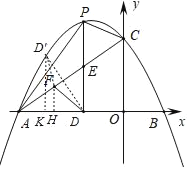
����Ϊ��H������D����D��K��x�ᣬ����Ϊ��K������D��F��
��Rt��AFH��FH��![]() ��
��
��![]() ��
��
��D����F��H���㹲������D��K�غ�ʱ��D��F+FHȡ����Сֵ![]() ��
��
��3����A����6��0����C��0��2![]() ������G��AC�е㣬
������G��AC�е㣬
��![]() ����AOC��60����
����AOC��60����
������á�COC����60����
��AC��OC����
��ֱ��OC���Ľ���ʽΪy��![]() ��
��
��H��m��![]() ����
����
�ߡ�BOB����60����B��2��0����
��![]() ��
��
����GHB��Ϊ����������ʱ��
����GH��GB����![]() ��
��
�����ã�m2+3m��12��0��
��ã�m��![]() ��
��
��H1![]() ��
��
����HB����GH��![]() ��
��
���m����2��
��![]() ��
��
����HB����GB����![]() ��
��
������m2��18��
���m=��3![]() ��
��
��H4��3![]() ��
��![]() ����H5��-3
����H5��-3![]() ��-
��-![]() ����
����
�ۺ����Ͽɵõ�H������Ϊ����2����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����3
����3![]() ��
��![]() ����-3
����-3![]() ��-
��-![]() ����
����


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��˼�������ˮ���죬�����ƽ�ˮ��Դ��Լ����2019��1��1�������������ij�������������ˮ�Ľ���ˮ�������ӡ��¼������ɷѵ���Ϊ����������ɷѰ���һ��һ�����������ͥΪ3���˼��㣬������ˮ����ˮ�ۼ��±���
����ˮ�����֣� | ˮ�ۣ�Ԫ/�֣� | |
��һ���� | 0��216����216�� |
|
�ڶ����� | 216��288����288�� |
|
�������� | 288���� | 8.4 |
С���Һ�С�ռҾ�Ϊ3��֮�ң�2018��ȫ����ˮ���ֱ�Ϊ260�ֺ�300�֣���������������ɷѱ����㣬С���Һ�С�ռ�ȫ��Ӧ��ˮ�ѷֱ�Ϊ789.6Ԫ��1008Ԫ.
��1�������![]() ��
��![]() ��ֵ��
��ֵ��
��2��С�ռ�ʵʩ��ˮ�ƻ�����2018����ˮ��Ϊ��㣬Ԥ��2020����ˮ������243�֣��Ҵ�2018�굽2020��ÿ����ˮ����ƽ���½��ʶ���ͬ���밴���½��ʼ���2021��С�ռ���ˮ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ����������
����������![]() ��
��![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĶԳ�ͼ��
�ĶԳ�ͼ��![]() .
.

��1����![]() �������ı���
�������ı���![]() ��������ֵ��
��������ֵ��
��2������![]() ǡ������
ǡ������![]() ���ϣ�����
���ϣ�����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������һ��С�γ�ͬʱ�Ӽس���������������ʻ���ҵأ�С�γ���;ͣ������2h��������ʻ���ҵأ�����ʻʱ��Ϊx�� h����������·��Ϊy1�� km����С�γ���·��Ϊy2�� km ����ͼ�е��߶�OA������OBCD�ֱ��ʾy1��y2��x֮��ĺ�����ϵ��
��1�������������_____km��m=_____��
��2�����߶�CD����ֱ�ߵĺ�������ʽ��
��3��С�γ�ͣ��������Ҫ������ʻ����Сʱ�������֮�����20km��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ��ÿ������A��B����Ʒ�Ƶı���Ʒ��600ƿ��A��B���ֲ�Ʒÿƿ�ijɱ����ۼ����±�����ÿ������A��Ʒxƿ�����������ֲ�Ʒÿ�칲����yԪ��
A | ��B | |
�ɱ���Ԫ��/ƿ | 50 | ��35 |
�ۼۣ�Ԫ��/ƿ | 70 | ������50 |
��1�������y����x�ĺ�����ϵ��
��2���ó�ÿ��������A��B���ֲ�Ʒ��ij������ȫ�����������Ҷ�B��Ʒ���䣬��A��Ʒ����������ÿƿ����![]() Ԫ���������������ʹÿ����������������Ƕ��٣�
Ԫ���������������ʹÿ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2����ͬ�ĵ�ӰA��B���ס��ҡ���3�˷ֱ��������ѡ��1���ۿ�.
��1�����ѡ��A����Ӱ�ĸ��ʣ�
��2����ס��ҡ���3��ѡ��ͬһ����Ӱ�ĸ��ʣ����û���״ͼ�ķ��������������̣�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Сһ�����������Σ��ɰ����з�ʽ����ƴ�ӣ�
��ʽ1����ͼ1��
��ʽ2����ͼ2��
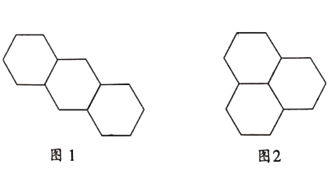
�����ĸ��߳���Ϊ1���������Σ����÷�ʽ1ƴ�ӣ�����ͼ�������������ܳ���_______.��![]() ���߳���Ϊ1���������Σ������������ַ�ʽ��һ�ֻ����ַ�ʽ���ƴ�ӣ�����ͼ�������������ܳ�Ϊ18����
���߳���Ϊ1���������Σ������������ַ�ʽ��һ�ֻ����ַ�ʽ���ƴ�ӣ�����ͼ�������������ܳ�Ϊ18����![]() �����ֵΪ__________��
�����ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����IJ�������⣺
��1��С�������п�Ƭ�Ϸֱ���1��2��3��4��С�������п�Ƭ�Ϸֱ����1��2��3���ֱ���a��b��ʾС����С����С�������г���Ŀ�Ƭ�ϱ��е����֣�������״ͼ�����б���д����a��b��������ȡֵ�����
��2����a��b���ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�ÿ��������60Ԫ��ÿ��������80Ԫ.���ۼ�Ϊÿ��60Ԫ�ǣ�ÿ���¿�����100�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������2��.��ÿ����Ʒ���ۼ�Ϊ![]() Ԫ��
Ԫ��![]() Ϊ����������ÿ���µ���������Ϊ
Ϊ����������ÿ���µ���������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ��
��![]() �ĺ�����ϵʽ��ֱ��д���Ա���
�ĺ�����ϵʽ��ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
��3����ÿ����Ʒ����Ϊ����Ԫʹ��ÿ���µ�����ǡΪ2250Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com