
【题目】如图,已知![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() .
.

(1)若![]() ,试求四边形
,试求四边形![]() 面积的最大值;
面积的最大值;
(2)若点![]() 恰好落在
恰好落在![]() 轴上,试求
轴上,试求![]() 的值.
的值.
科目:初中数学 来源: 题型:
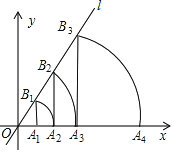
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红的父母开了一个小服装店,出售某种进价为![]() 元的服装,现每件
元的服装,现每件![]() 元,每星期可卖
元,每星期可卖![]() 件.该同学对市场作了如下调查:每降价
件.该同学对市场作了如下调查:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件;每涨价
件;每涨价![]() 元,每星期要少卖
元,每星期要少卖![]() 件.
件.
![]() 小红已经求出在涨价情况下一个星期的利润
小红已经求出在涨价情况下一个星期的利润![]() (元)与售价
(元)与售价![]() (元)(
(元)(![]() 为整数)的函数关系式为
为整数)的函数关系式为![]() ,请你求出在降价的情况下
,请你求出在降价的情况下![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为
在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为![]() 元?
元?
![]() 问如何定价,才能使一星期获得的利润最大?
问如何定价,才能使一星期获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
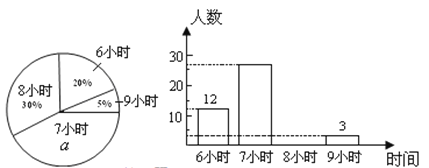
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
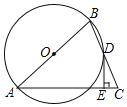
【题目】如图,在![]() 中,
中,![]() ,点D在BC上,
,点D在BC上,![]() ,过点D作
,过点D作![]() ,垂足为E,
,垂足为E,![]() 经过A,B,D三点.
经过A,B,D三点.
![]() 求证:AB是
求证:AB是![]() 的直径;
的直径;
![]() 判断DE与
判断DE与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
![]() 若
若![]() 的半径为10m,
的半径为10m,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连接AC.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连接AC.
(1)求直线AC的解析式;
(2)如图1,点P为直线AC上方抛物线上一动点,过P作PD⊥AB,交AC于点E,点F是线段AC上一动点,连接DF.当△PAC的面积最大时,求DF+![]() AF的最小值;
AF的最小值;
(3)如图2,将△OBC绕着点O顺时针旋转60°得△OB′C′,点G是AC中点,点H为直线OC′上一动点,当△GHB′为等腰三角形时,直接写出对应的点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是( )
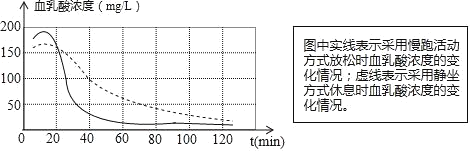
A. 运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B. 运动员高强度运动后,最高血乳酸浓度大约为250mg/L
C. 采用慢跑活动方式放松时,运动员必须慢跑70min后才能基本消除疲芳
D. 运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com