
����Ŀ�������о���������Ѫ����Ũ���������˶���о�ƣ�͵���Ҫԭ���˶�Աδ�˶�ʱ������Ѫ����Ũ��ˮƽͨ����40mg/L���£����Ѫ����Ũ�Ƚ���50mg/L���£��˶�Ա�ͻ���������ƣ�ͣ��������й����߸���ʵ�����ݣ�������һ��ͼ������ӳ���˶�Ա���и�ǿ���˶�������Ѫ����Ũ����ʱ��仯���仯�ĺ�����ϵ������������ȷ���ǣ�������
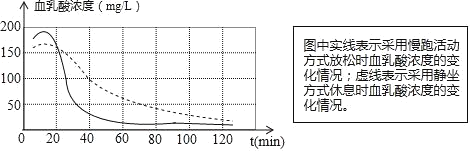
A. �˶���40minʱ���������ܻ��ʽ����ʱ��Ѫ����Ũ������þ�����ʽ��Ϣʱ��Ѫ����Ũ����ͬ
B. �˶�Ա��ǿ���˶������Ѫ����Ũ�ȴ�ԼΪ250mg/L
C. �������ܻ��ʽ����ʱ���˶�Ա��������70min����ܻ�������ƣ��
D. �˶�Ա����������˶���Ϊ�˸���ﵽ����ƣ�͵�Ч����Ӧ�ò������ܻ��ʽ������
���𰸡�D
��������
���ݺ���ͼ����������ʾ�������жϼ��ɣ�
A���˶���40minʱ���������ܻ��ʽ����ʱ��Ѫ����Ũ������þ�����ʽ��Ϣʱ��Ѫ����Ũ�Ȳ�ͬ������
B���˶�Ա��ǿ���˶������Ѫ����Ũ�ȴ�ԼΪ200mg/L������
C���������ܻ��ʽ����ʱ���˶�Ա��������40min����ܻ�������ƣ�ͣ�����
D���˶�Ա����������˶���Ϊ�˸���ﵽ����ƣ�͵�Ч����Ӧ�ò������ܻ��ʽ�����ɣ���ȷ��
��ѡD��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ����������
����������![]() ��
��![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĶԳ�ͼ��
�ĶԳ�ͼ��![]() .
.

��1����![]() �������ı���
�������ı���![]() ��������ֵ��
��������ֵ��
��2������![]() ǡ������
ǡ������![]() ���ϣ�����
���ϣ�����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Сһ�����������Σ��ɰ����з�ʽ����ƴ�ӣ�
��ʽ1����ͼ1��
��ʽ2����ͼ2��
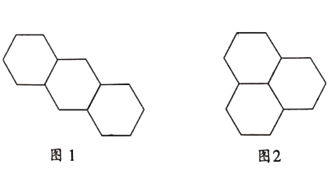
�����ĸ��߳���Ϊ1���������Σ����÷�ʽ1ƴ�ӣ�����ͼ�������������ܳ���_______.��![]() ���߳���Ϊ1���������Σ������������ַ�ʽ��һ�ֻ����ַ�ʽ���ƴ�ӣ�����ͼ�������������ܳ�Ϊ18����
���߳���Ϊ1���������Σ������������ַ�ʽ��һ�ֻ����ַ�ʽ���ƴ�ӣ�����ͼ�������������ܳ�Ϊ18����![]() �����ֵΪ__________��
�����ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����IJ�������⣺
��1��С�������п�Ƭ�Ϸֱ���1��2��3��4��С�������п�Ƭ�Ϸֱ����1��2��3���ֱ���a��b��ʾС����С����С�������г���Ŀ�Ƭ�ϱ��е����֣�������״ͼ�����б���д����a��b��������ȡֵ�����
��2����a��b���ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD������AD����E��AD���е㣬����BE���ӳ���CD��F�㣮
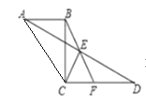
��1����˵����ABE�ա�DFE�����ɣ�
��2������CE��AC,��CB��CD��AC=CD,��D=30����CD=2����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���������y��![]() ��ͼ�����A��6��1����
��ͼ�����A��6��1����
��1���������ı���ʽ��
��2������A��ֱ���뷴������y��![]() ͼ�����һ������ΪB����y�ύ�㽻�ڵ�P��
ͼ�����һ������ΪB����y�ύ�㽻�ڵ�P��
������PΪԭ�㣬ֱ��д����B�����ꣻ
����PA��2PB�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��ѧ���ü�����������Ϊÿ̨20Ԫ���ۼ�Ϊÿ̨30Ԫʱ��ÿ�ܿ���160̨�����ÿ̨�ۼ�ÿ����2Ԫ��ÿ�ܾͻ�����20̨�������ҹ涨���ÿ̨�ۼ۲��ܳ���33Ԫ��������������Ϊ����Ԫʱ���̳�ÿ�ܵ�����ǡ��Ϊ1680Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�ÿ��������60Ԫ��ÿ��������80Ԫ.���ۼ�Ϊÿ��60Ԫ�ǣ�ÿ���¿�����100�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������2��.��ÿ����Ʒ���ۼ�Ϊ![]() Ԫ��
Ԫ��![]() Ϊ����������ÿ���µ���������Ϊ
Ϊ����������ÿ���µ���������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ��
��![]() �ĺ�����ϵʽ��ֱ��д���Ա���
�ĺ�����ϵʽ��ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
��3����ÿ����Ʒ����Ϊ����Ԫʹ��ÿ���µ�����ǡΪ2250Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
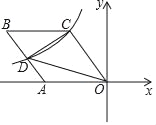
����Ŀ����ͼ������OABC��һ��OA��x��ĸ������ϣ�O������ԭ�㣬tan��AOC=![]() ������������y=��
������������y=��![]() ��ͼ����C����AB�����D������COD�������ֵ����_____��
��ͼ����C����AB�����D������COD�������ֵ����_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com